| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
C.8.3 Generalized Newton identities
The error-locator polynomial is defined by
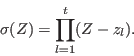
If this product is expanded,
then the coefficients
Generalized Newton identities
The syndromes
![]() and the coefficients
and the coefficients ![]() satisfy
the following generalized Newton identities:
satisfy
the following generalized Newton identities:
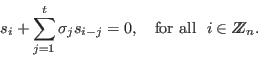
Decoding up to error-correcting capacity
We have
![]() , since
, since
![]() . Furthermore
. Furthermore
and
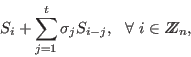
For an example see sysNewton in decodegb_lib. More on this method and the method based on
Waring function can be found in [ABF2002]. See also [ABF2008].