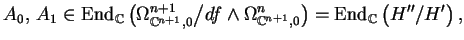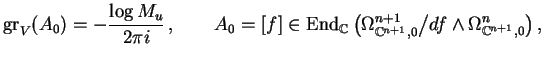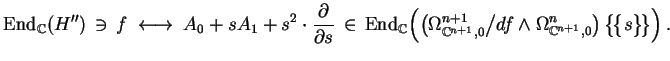|
|
%body
|
%body
|
|
%body
|

|
%body
|
SINGULAR - A Computer Algebra System for Polynomial Computations
Overview
Objects
Functionality
Libraries
Examples
Applications
Availability
History
Contributors
Future
%body
|
|
Sao Carlos, 08/02
|
http://www.singular.uni-kl.de
|
SINGULAR Examples
Build. Blocks
Comb. Appl.
HCA Proving
Arrangements
Branches
Classify
Coding
Deformations
Equidim Part
Existence
Finite Groups
Flatness
Genus
Hilbert Series
Membership
Nonnormal Locus
Normalization
Primdec
Puiseux
Plane Curves
Saturation
Solving
Space Curves
Spectrum
%body
|
|
Sao Carlos, 08/02
|
http://www.singular.uni-kl.de
|
SINGULAR Applications
| Task: |
Compute M. Saito's endomorphisms
which satisfy:
A1 is semisimple with eigenvalues being the spectral
numbers of f added by 1, and
|
ring R=0,(x,y),ds;
poly f=x5+x2y2+y5;
LIB "gaussman.lib";
The command tmatrix(f) returns a list
L :
-
L[1] contains
A0 with respect to the basis
matrix(L[4])*L[3] of H''/H'.
-
L[2] contains
A1 with respect to the basis
matrix(L[4])*L[3] of H''/H'.
-
L[4] contains a monomial vector space basis for
H''/H'.
list L=tmatrix(f);
print(L[1]); // the matrix A_0
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
1,0,0,0,0,0,0,0,0,0,0
print(L[2]); // the matrix A_1
1/2,0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 7/10,0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 7/10,0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 9/10,0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 9/10,0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 11/10,0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 11/10,0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 13/10,0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 13/10,0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3/2
print(matrix(L[4])*L[3]); // the chosen basis of H''/H'
-1+2xy-1445/64y5, 16x+125y4, 16y+125x4, 4x2+5y3, 4y2+5x3, xy+85/8y5, y3, x3, y4, x4, 1/2y5