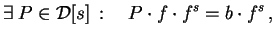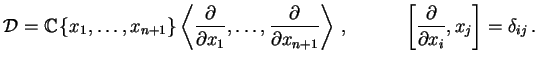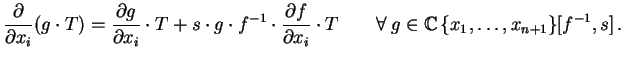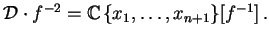==> %body 
==>
 
%body
%body
%body %body
%body %body %body
%body SINGULAR - A Computer Algebra System for Polynomial Computations Overview Objects Functionality Libraries Examples Applications Availability History Contributors Future %body
Sao Carlos, 08/02 http://www.singular.uni-kl.de
SINGULAR Examples Build. Blocks Comb. Appl. HCA Proving
Arrangements Branches Classify Coding Deformations Equidim Part Existence Finite Groups Flatness Genus Hilbert Series Membership Nonnormal Locus Normalization Primdec Puiseux Plane Curves Saturation Solving Space Curves Spectrum %body
Sao Carlos, 08/02 http://www.singular.uni-kl.de
SINGULAR Applications Robotics Circuit Design Medicine Glass Melting %body
Sao Carlos, 08/02 http://www.singular.uni-kl.de
Task: Compute the roots of the (local) Bernstein polynomial  b = b(s), the minimal non-trivial complex polynomial, which satisfies
where
Here,   fs   is a formal notation for an indeterminate T on which we have the following actions:

Note that the roots of b are negative rational numbers and -1 is a root of b. To compute the roots of the Bernstein polynomial b excluding the root -1, we type:

ring R=0,(x,y),ds;
poly f=x5+x2y2+y5;
LIB "gaussman.lib";
bernstein(f); // an implementation based on Malgrange's results
_[1]=-1/2 _[2]=-7/10 _[3]=-9/10 _[4]=-11/10 _[5]=-13/10 In particular, since -2 is smaller than all roots of the Bernstein polynomial of f, we have