
==>
|
%body
|
==> |
%body |

|
|
|
| Sao Carlos, 08/02 | http://www.singular.uni-kl.de |
|
|
|
| Sao Carlos, 08/02 | http://www.singular.uni-kl.de |
|
|
|
| Sao Carlos, 08/02 | http://www.singular.uni-kl.de |
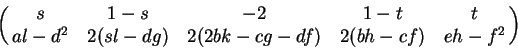
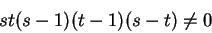 .
.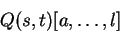 .
.