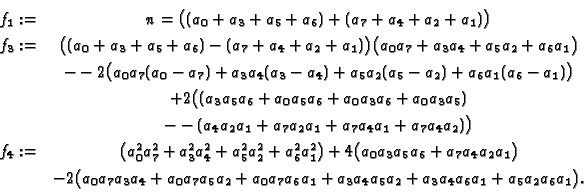| Robotics |
| Circuit Design |
| Medicine |
| Glass Melting |
Equations
Let ![]() be the rate measuring the exposure to natural infection
with disease
be the rate measuring the exposure to natural infection
with disease ![]() (exposition factor),
(exposition factor),
![]() the proportion of children previously with no detectable
antibodies to disease
the proportion of children previously with no detectable
antibodies to disease![]() who acquire
who acquire
detectable antibodies to disease
![]() when vaccinated (seroconversion).
when vaccinated (seroconversion).
Then
![]() measures the presence of antibodies
to disease
measures the presence of antibodies
to disease![]() under vaccination
under vaccination
conditions.
From these data it is possible to obtain information about the
expected antibody prevalence in general.
Let
![]() with
with ![]() (resp.
(resp. ![]() ) at the
) at the ![]() -th place standing for the presence (resp. absence) of
antibodies
-th place standing for the presence (resp. absence) of
antibodies
to the
![]() -th disease. Through laboratory testing the eight values
-th disease. Through laboratory testing the eight values
![]() are
are
known. We obtain the following equations:
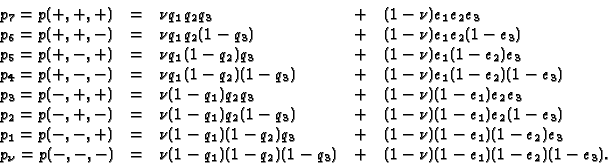
After the (technical) substitution
eliminated. The result is a quadratic equation:
Using the factorization of SINGULAR we obtain
This leads to the following formula:
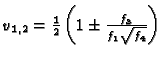 with
with