|
|
D.4.19.8 diagInvariants
Procedure from library normaliz.lib (see normaliz_lib).
- Usage:
- diagInvariants(intmat A, intmat U);
diagInvariants(intmat A, intmat U, intvec grading);
- Return:
- This function computes the ring of invariants of a diagonalizable group
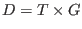 where where 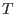 is a torus and is a torus and 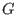 is a finite abelian group, both
acting diagonally on the polynomial ring is a finite abelian group, both
acting diagonally on the polynomial ring
![$K[X_1,\ldots,X_n]$](sing_920.png) . The group
actions are specified by the input matrices A and U. The first matrix specifies
the torus action, the second the action of the finite group. See
torusInvariants and finiteDiagInvariants for more detail. The output is a
monomial ideal listing the algebra generators of the subalgebra of invariants. . The group
actions are specified by the input matrices A and U. The first matrix specifies
the torus action, the second the action of the finite group. See
torusInvariants and finiteDiagInvariants for more detail. The output is a
monomial ideal listing the algebra generators of the subalgebra of invariants.
The function returns the ideal given by the input matrix A if one of
the options supp, triang, volume, or
hseries has been activated.
However, in this case some numerical invariants are computed, and
some other data may be contained in files that you can read into
Singular (see showNuminvs, exportNuminvs).
Example:
| | LIB "normaliz.lib";
ring R=0,(x,y,z,w),dp;
intmat E[2][4] = -1,-1,2,0, 1,1,-2,-1;
intmat C[2][5] = 1,1,1,1,5, 1,0,2,0,7;
diagInvariants(E,C);
==> _[1]=x4y6z5
==> _[2]=x15y5z10
==> _[3]=xy19z10
==> _[4]=x26y4z15
==> _[5]=x37y3z20
==> _[6]=x48y2z25
==> _[7]=x59yz30
==> _[8]=x70z35
==> _[9]=y70z35
|
See also:
finiteDiagInvariants;
intersectionValRingIdeals;
intersectionValRings;
torusInvariants.
|








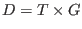 where
where 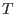 is a torus and
is a torus and 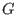 is a finite abelian group, both
acting diagonally on the polynomial ring
is a finite abelian group, both
acting diagonally on the polynomial ring
![$K[X_1,\ldots,X_n]$](sing_920.png) . The group
actions are specified by the input matrices A and U. The first matrix specifies
the torus action, the second the action of the finite group. See
torusInvariants and finiteDiagInvariants for more detail. The output is a
monomial ideal listing the algebra generators of the subalgebra of invariants.
. The group
actions are specified by the input matrices A and U. The first matrix specifies
the torus action, the second the action of the finite group. See
torusInvariants and finiteDiagInvariants for more detail. The output is a
monomial ideal listing the algebra generators of the subalgebra of invariants.