| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
7.3.14 modulo (plural)
Syntax:modulo (ideal_expression,ideal_expression)modulo (module_expression,module_expression)Type:- module
Purpose:modulo(h1,h2)represents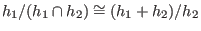 , where
, where
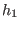 and
and 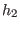 are considered as submodules of the same free module
are considered as submodules of the same free module
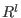 (l=1 for ideals).
(l=1 for ideals).
Let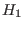 (resp.
(resp. 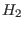 ) be the matrix of size
) be the matrix of size 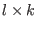 (resp.
(resp. 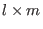 ), having the
generators of
), having the
generators of 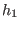 (resp.
(resp. 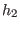 )as columns.
)as columns.
Then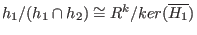 , where
, where
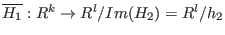 is the induced map given by
is the induced map given by
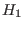 .
.modulo(h1,h2)returns generators of the kernel of this induced map.Note: If, for at least one of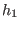 or
or 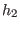 ,the attribute
,the attribute isHomogis st, thenmodulo(h1,h2)also sets this attribute (if the weights are compatible).Example:LIB "ncalg.lib"; def A = makeUsl2(); setring A; // this algebra is U(sl_2) option(redSB); option(redTail); ideal H2 = e2,f2,h2-1; H2 = twostd(H2); print(matrix(H2)); // print H2 in a compact form ==> h2-1,fh-f,eh+e,f2,2ef-h-1,e2 ideal H1 = std(e); ideal T = modulo(H1,H2); T = NF(std(H2+T),H2); T = std(T); T; ==> T[1]=h-1 ==> T[2]=e