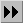|
|
C.2 Hilbert function
Let M
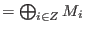 be a graded module over be a graded module over ![$K[x_1,..,x_n]$](sing_539.png) with
respect to weights with
respect to weights 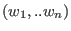 .
The Hilbert function of .
The Hilbert function of 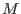 , , 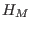 , is defined (on the integers) by , is defined (on the integers) by
The Hilbert-Poincare series of 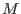 is the power series is the power series
It turns out that
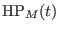 can be written in two useful ways
for weights can be written in two useful ways
for weights 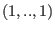 : :
where 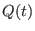 and and 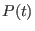 are polynomials in are polynomials in ![${\bf Z}[t]$](sing_549.png) . .
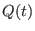 is called the first Hilbert series,
and is called the first Hilbert series,
and 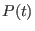 the second Hilbert series.
If the second Hilbert series.
If
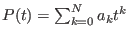 , and , and 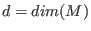 ,
then ,
then
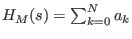
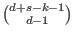 (the Hilbert polynomial) for
(the Hilbert polynomial) for 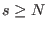 . .
Generalizing this to quasihomogeneous modules we get
where 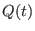 is a polynomial in is a polynomial in ![${\bf Z}[t]$](sing_549.png) . .
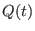 is called the first (weighted) Hilbert series of M. is called the first (weighted) Hilbert series of M.
|