| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
C.8.1 Codes and the decoding problem
Codes
-
Let
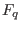 be a field with
be a field with 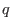 elements. A linear code
elements. A linear code 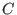 is a linear subspace of
is a linear subspace of 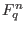 endowed with the
Hamming metric.
endowed with the
Hamming metric. -
Hamming distance between x,y
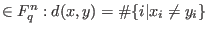 .
Hamming weight of x
.
Hamming weight of x
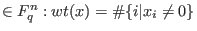 .
. -
Minimum distance of the code
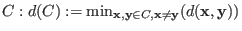 .
. -
The code
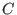 of dimension
of dimension 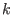 and minimum distance
and minimum distance 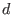 is denoted as
is denoted as ![$[n,k,d]$](sing_702.png) .
. -
A matrix
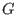 whose rows are the base vectors of
whose rows are the base vectors of 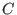 is the generator matrix.
is the generator matrix. -
A matrix
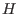 with the property
with the property
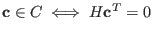 is the check matrix.
is the check matrix.
Cyclic codes
The codeA cyclic code has several defining sets.
Decoding problem
-
Complete decoding: Given
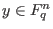 and a code
and a code
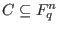 , so that
, so that 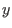 is at distance
is at distance 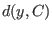 from
the code, find
from
the code, find
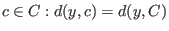 .
. -
Bounded up to half the minimum distance: With the additional assumption
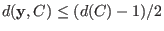 , a codeword with the above property
is unique.
, a codeword with the above property
is unique.
Decoding via systems solving
One distinguishes between two concepts:-
Generic decoding: Solve some system
 and obtain some "closed" formulas
and obtain some "closed" formulas 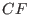 . Evaluating these formulas
at data specific to a received word
. Evaluating these formulas
at data specific to a received word 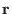 should yield a solution to the decoding problem. For example for
should yield a solution to the decoding problem. For example for
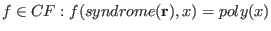 . The roots of
. The roots of 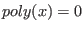 yield error positions, see the section on the
general error-locator polynomial.
yield error positions, see the section on the
general error-locator polynomial. -
Online decoding: Solve some system
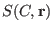 . The solutions should solve the decoding problem.
. The solutions should solve the decoding problem.
Computational effort
- Generic decoding. Here, preprocessing is very hard, whereas decoding is relatively simple (if the formulas are sparse).
- Online decoding. In this case, decoding is the hard part.