Singular Manual: Fitzgerald-Lax method

Forward: Decoding method based on quadratic equations

C.8.4 Fitzgerald-Lax method

Affine codes

Let $I=\langle g_1,\dots,g_m \rangle \subseteq F_q[X_1,\dots,X_s]$ be an ideal. Define

$\begin{displaymath} I_q:=I+\langle X_1^q-X_1,\dots,X_s^q-X_s\rangle . \end{displaymath}$

is a zero-dimensional ideal. Define also $V(I_q)=:\{P_1,\dots,P_n\}$ . Every

-ary linear code

with parameters

can be seen as an affine variety code

, that is, the image of a vector space

of the evaluation map

$\begin{displaymath} \phi :R\to F_q ^n \end{displaymath}$

$\begin{displaymath} \bar{f}\mapsto(f(P_1),\dots,f(P_n)), \end{displaymath}$

where $R:=F_q[U_1,\dots,U_s]/I_q$ ,

is a vector subspace of

and $\bar{f}$ the coset of

in $F_q[U_1,\dots,U_s]$ modulo

Decoding affine variety codes

Given a -ary code with a generator matrix $G=(g_{ij})$ :

choose 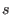, such that 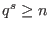$q^s\ge n$ , and construct 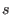distinct points 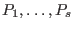$P_1,\dots,P_s$ in .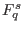
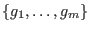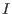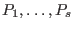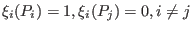Construct a Gröbner basis $\{g_1,\dots,g_m\}$ for an ideal of polynomials from $F_q[X_1,\dots,X_s]$ that vanish at the points $P_1,\dots,P_s$ . Define $\xi_i\in F_q[X_1,\dots,X_s]$ such that $\xi_i(P_i)=1,\xi_i(P_j)=0,i\ne j$ .
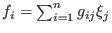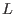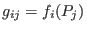Then $f_i=\sum_{i=1}^ng_{ij}\xi_j$ span the space , so that $g_{ij}=f_i(P_j)$ .

In this way we obtain that the code is the image of the evaluation above, thus . In the same way by considering a parity check matrix instead of a generator matrix we have that the dual code is also an affine variety code.

The method of decoding is a generalization of CRHT. One needs to add polynomials $(g_l(X_{k1},\dots,X_{ks}))_{l=1,\dots,m; k=1,\dots,t}$ for every error position. We also assume that field equations on $X_{ij}$ 's are included among the polynomials above. Let be a -ary linear code such that its dual is written as an affine variety code of the form $C^{\bot}=C(I,L)$ . Let ${\bf r}={\bf c}+{\bf e}$ as usual and $t\le e$ . Then the syndromes are computed by $s_i=\sum_{j=1}^nr_jf_i(P_j)=\sum_{j=1}^ne_jf_i(P_j) \hbox{ for } i=1,\dots,n-k$ .

Consider the ring $F_q[X_{11},\dots,X_{1s},\ldots,X_{t1},\dots,X_{ts},E_1,\dots,E_t]$ , where $(X_{i1},\dots,X_{is})$ correspond to the -th error position and to the -th error value. Consider the ideal generated by

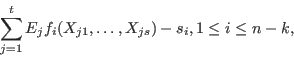
$\begin{displaymath} \sum_{j=1}^tE_jf_i(X_{j1},\dots,X_{js})-s_i, 1\le i\le n-k, \end{displaymath}$

$\begin{displaymath} g_l(X_{j1},\dots,X_{js}), 1\le l\le m, \end{displaymath}$

$\begin{displaymath} E_k^{q-1}-1. \end{displaymath}$

Theorem:: Let 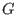be the reduced Gröbner basis for 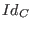with respect to an elimination order 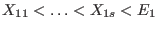$X_{11}<\dots<X_{1s}<E_1$ . Then we may solve for the error locations and values by applying elimination theory to the polynomials in .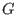

For an example see sysFL in decodegb_lib. More on this method can be found in [FL1998].

User manual for Singular version 4-0-3, 2016, generated by texi2html.