Singular Manual: Generalized Newton identities

C.8.3 Generalized Newton identities

The error-locator polynomial is defined by

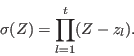
$\begin{displaymath} \sigma(Z)=\prod_{l=1}^{t}(Z-z_l). \end{displaymath}$

If this product is expanded,

$\begin{displaymath} \sigma(Z)=Z^t+\sigma_1Z^{t-1}+\dots+\sigma_{t-1}Z+\sigma_t, \end{displaymath}$

then the coefficients $\sigma_i$ are the elementary symmetric functions in the error locations $z_1,\dots,z_t$

$\begin{displaymath} \sigma_i=(-1)^i\sum_{1\le j_1<j_2<\dots<j_i\le t}z_{j_1}z_{j_2}\dots z_{j_i}, \ 1\le i\le t. \end{displaymath}$

Generalized Newton identities

The syndromes and the coefficients $\sigma_i$ satisfy the following generalized Newton identities:

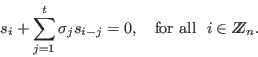
$\begin{displaymath} s_i+\sum_{j=1}^{t}\sigma_js_{i-j}=0,\ \ \hbox{ for all } \ i\in Z\!\!\! Z_n. \end{displaymath}$

Decoding up to error-correcting capacity

We have $s_{i+n}=s_i, \hbox{ for all } i\in Z\!\!\! Z_n$ , since $s_{i+n}=r(a^{i+n})=r(a^i)$ . Furthermore

$\begin{displaymath} s_i^q=(e(a^i))^q=e(a^{iq})=s_{qi}, \hbox{ for all } i \in Z_n, \end{displaymath}$

and $\sigma_i^{q^m}=\sigma_i, \hbox{ for all } 1\le i \le t$ . Replace the syndromes by variables and obtain the following set of polynomials

in the variables $S_1,\dots,S_n$ and $\sigma_1,\dots,\sigma_t$ :

$\begin{displaymath} \sigma_i^{q^m}-\sigma_i, \ \ \forall \ 1\le i \le t, \end{displaymath}$

$\begin{displaymath} S_{i+n}-S_i, \ \ \forall \ i\in Z\!\!\! Z_n, \end{displaymath}$

$\begin{displaymath} S_i^q-S_{qi}, \ \ \forall \ i\in Z\!\!\! Z_n, \end{displaymath}$

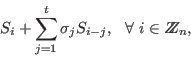
$\begin{displaymath} S_i+\sum_{j=1}^{t}\sigma_jS_{i-j}, \ \ \forall \ i\in Z\!\!\! Z_n, \end{displaymath}$

$\begin{displaymath} S_i-s_i(r) \ \ \forall \ i\in S_C. \end{displaymath}$

For an example see sysNewton in decodegb_lib. More on this method and the method based on Waring function can be found in [ABF2002]. See also [ABF2008].

User manual for Singular version 4.3.1, 2022, generated by texi2html.