|
|
5.1.125 quotient
Syntax:
quotient ( ideal_expression, ideal_expression )
quotient ( module_expression, module_expression )
Type:
- ideal
Syntax:
quotient ( module_expression, ideal_expression )
Type:
- module
Purpose:
- computes the ideal quotient, resp. module quotient. Let
R be the
basering, I,J ideals and M a module in
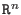 .Then .Then
-
quotient(I,J)=
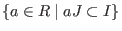 , , -
quotient(M,J)=
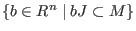 . .
Example:
| | ring r=181,(x,y,z),(c,ls);
ideal id1=maxideal(3);
ideal id2=x2+xyz,y2-z3y,z3+y5xz;
ideal id6=quotient(id1,id2);
id6;
==> id6[1]=z
==> id6[2]=y
==> id6[3]=x
quotient(id2,id1);
==> _[1]=z2
==> _[2]=yz
==> _[3]=y2
==> _[4]=xz
==> _[5]=xy
==> _[6]=x2
module m=x*freemodule(3),y*freemodule(2);
ideal id3=x,y;
quotient(m,id3);
==> _[1]=[1]
==> _[2]=[0,1]
==> _[3]=[0,0,x]
|
See
fglmquot;
ideal;
modQuotient;
module.
|





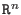 .Then
.Then
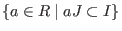 ,
,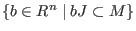 .
.