|
|
7.3.22 quotient (plural)
Syntax:
quotient ( ideal_expression, ideal_expression )
quotient ( module_expression, module_expression )
Type:
- ideal
Syntax:
quotient ( module_expression, ideal_expression )
Type:
- module
Purpose:
- computes the ideal quotient, resp. module quotient. Let
R be the
basering, I,J ideals and M, N submodules in
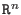 .Then .Then
-
quotient(I,J)=
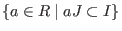 , , -
quotient(M,J)=
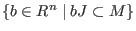 . .
Note:
- It can only be used for two-sided ideals (bimodules) in the second argument, otherwise the
result may have no meaning.
Example:
| | //------ a very simple example ------------
ring r=(0,q),(x,y),Dp;
def R=nc_algebra(q,0); // this algebra is a quantum plane
setring R;
option(returnSB);
poly f1 = x^3+2*x*y^2+2*x^2*y;
poly f2 = y;
poly f3 = x^2;
poly f4 = x+y;
ideal i = f1,f2;
ideal I = twostd(i);
ideal j = f3,f4;
ideal J = twostd(j);
quotient(I,J);
==> _[1]=y
==> _[2]=x2
module M = x*freemodule(3), y*freemodule(2);
quotient(M, ideal(x,y));
==> _[1]=gen(1)
==> _[2]=gen(2)
==> _[3]=x*gen(3)
kill r,R;
//------- a bit more involved example
LIB "ncalg.lib";
def Usl2 = makeUsl2();
// this algebra is U(sl_2)
setring Usl2;
ideal i = e3,f3,h3-4*h;
ideal I = std(i);
poly C = 4*e*f+h^2-2*h;
ideal H = twostd(C-8);
option(returnSB);
ideal Q = quotient(I,H);
// print a compact presentation of Q:
print(matrix(Q));
==> h,f3,ef2-4f,e2f-6e,e3
|
See
ideal (plural);
module (plural).
|





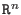 .Then
.Then
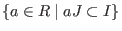 ,
,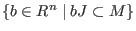 .
.