|
|
D.10.1.8 prepSV
Procedure from library brnoeth.lib (see brnoeth_lib).
- Usage:
- prepSV( G, D, F, EC ); G,D,F intvecs and EC a list
- Return:
- list E of size n+3, where n=size(D). All its entries but E[n+3]
are matrices:
| | E[1]: parity check matrix for the current AG code
E[2] ... E[n+2]: matrices used in the procedure decodeSV
E[n+3]: intvec with
E[n+3][1]: correction capacity
of the algorithm
E[n+3][2]: designed Goppa distance
of the current AG code
|
- Note:
- Computes the preprocessing for the basic (Skorobogatov-Vladut)
decoding algorithm.
The procedure must be called within the ring EC[1][4], where EC is
the output of extcurve(d) (or in the ring EC[1][2] if d=1)
The intvec G and F represent rational divisors (see
BrillNoether for more details).
The intvec D refers to rational places (see AGcode_Omega
for more details.).
The current AG code is AGcode_Omega(G,D,EC).
If you know the exact minimum distance d and you want to use it in
decodeSV instead of
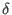 , you can change the value
of E[n+3][2] to d before applying decodeSV. , you can change the value
of E[n+3][2] to d before applying decodeSV.
If you have a systematic encoding for the current code and want to
keep it during the decoding, you must previously permute D (using
permute_L(D,P);), e.g., according to the permutation
P=L[3], L being the output of sys_code.
- Warnings:
- F must be a divisor with support disjoint from the support of D and
with degree
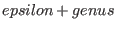 , where , where
![$epsilon:=[(deg(G)-3*genus+1)/2]$](sing_1063.png) . .
G should satisfy
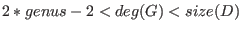 , which is
not checked by the algorithm. , which is
not checked by the algorithm.
G and D should also have disjoint supports (checked by the
algorithm).
Example:
| | LIB "brnoeth.lib";
int plevel=printlevel;
printlevel=-1;
ring s=2,(x,y),lp;
list HC=Adj_div(x3+y2+y);
==> The genus of the curve is 1
HC=NSplaces(1..2,HC);
HC=extcurve(2,HC);
==> Total number of rational places : NrRatPl = 9
def ER=HC[1][4];
setring ER;
intvec G=5; // the rational divisor G = 5*HC[3][1]
intvec D=2..9; // D = sum of the rational places no. 2..9 over F_4
// construct the corresp. residual AG code of type [8,3,>=5] over F_4:
matrix C=AGcode_Omega(G,D,HC);
==> Vector basis successfully computed
// we can correct 1 error and the genus is 1, thus F must have degree 2
// and support disjoint from that of D;
intvec F=2;
list SV=prepSV(G,D,F,HC);
==> Vector basis successfully computed
==> Vector basis successfully computed
==> Vector basis successfully computed
// now everything is prepared to decode with the basic algorithm;
// for example, here is a parity check matrix to compute the syndrome :
print(SV[1]);
==> 0,0,1, 1, (a), (a+1),(a+1),(a),
==> 0,1,(a),(a+1),(a), (a+1),(a), (a+1),
==> 1,1,1, 1, 1, 1, 1, 1,
==> 0,0,1, 1, (a+1),(a), (a), (a+1),
==> 0,0,(a),(a+1),(a+1),(a), 1, 1
// and here you have the correction capacity of the algorithm :
int epsilon=SV[size(D)+3][1];
epsilon;
==> 1
printlevel=plevel;
|
See also:
AGcode_Omega;
decodeSV;
extcurve;
permute_L;
sys_code.
|
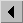





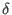 , you can change the value
of E[n+3][2] to d before applying decodeSV.
, you can change the value
of E[n+3][2] to d before applying decodeSV.
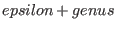 , where
, where
![$epsilon:=[(deg(G)-3*genus+1)/2]$](sing_1063.png) .
.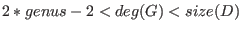 , which is
not checked by the algorithm.
, which is
not checked by the algorithm.