Singular Manual: Syzygies and resolutions (plural)

7.4.3 Syzygies and resolutions (plural)

Syzygies

Let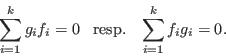

be a GR-algebra. A left (resp. right) syzygy between

elements $\{f_1,\dots,f_k\} \subset A^r$ is a

-tuple $(g_1,\dots ,g_k)\in A^k$ satisfying

$\begin{displaymath}\sum_{i=1}^{k} g_i f_i = 0 \;\;\; {\rm resp. } \;\;\; \sum_{i=1}^{k} f_i g_i = 0. \end{displaymath}$

The set of all left (resp. right) syzygies between $\{f_1,...,f_k\}$ is a left (resp. right) submodule

Remark: With respect to the definitions of ideal and module (see PLURAL), by syz PLURAL understands an inquiry to compute the left syzygy module.

Note, that rightModulo(M,std(0)) from nctools_lib computes the right syzygy module of M.

If S is a matrix of a left syzygy module of left submodule given by matrix M, then transpose(S)*transpose(M) = 0 (but, in general, $M \cdot S \not=0$ ).

Note, that the syzygy modules of depend on a choice of generators $\{g_1, \dots , g_s\}$ , but one can show that they depend on uniquely up to direct summands.

Free resolutions

Let $I={}_{A}\langle g_1,\dots ,g_s\rangle \subseteq A^r$ and

. A free resolution of is a long exact sequence

$\begin{displaymath}\dots \longrightarrow F_2 \buildrel{B_2}\over{\longrightarrow... ...1}\over{\longrightarrow} F_0\longrightarrow M\longrightarrow 0,\end{displaymath}$

with ${\tt transpose}(B_{i+1}) \cdot {\tt transpose}(B_i) =0$

and where the columns of the matrix generate . Note, that resolutions over factor-algebras need not to be of finite length.

Generalized Hilbert Syzygy Theorem

For a

-algebra

, generated by

variables, there exists a free resolution of length smaller or equal than

Example:

ring R=0,(x,y,z),dp;
matrix d[3][3];
d[1,2]=-z;  d[1,3]=2x;  d[2,3]=-2y;
def U=nc_algebra(1,d); // this algebra is U(sl_2)
setring U;
option(redSB); option(redTail);
ideal I=x3,y3,z3-z;
I=std(I);
I;
==> I[1]=z3-z
==> I[2]=y3
==> I[3]=x3
==> I[4]=y2z2-y2z
==> I[5]=x2z2+x2z
==> I[6]=x2y2z-2xyz2-2xyz+2z2+2z
resolution resI = mres(I,0);
resI;
==>  1      5      7      3      
==> U <--  U <--  U <--  U
==> 
==> 0      1      2      3      
==> 
list l = resI;
// The matrix A_1 is given by
print(matrix(l[1]));
==> z3-z,y3,x3,y2z2-y2z,x2z2+x2z
// We see that the columns of A_1 generate I.
// The matrix A_2 is given by
print(matrix(l[2]));
==> 0,        0,        y2,  x2,  6yz,        -36xy+18z+24,-6xz,       
==> z2+11z+30,0,        0,   0,   2x2z+12x2,  2x3,         0,          
==> 0,        z2-11z+30,0,   0,   0,          -2y3,        2y2z-12y2,  
==> -y,       0,        -z-5,0,   x2y-6xz-30x,9x2,         x3,         
==> 0,        -x,       0,   -z+5,-y3,        -9y2,        -xy2-4yz+28y
ideal tst; // now let us show that the resolution is exact
matrix TST;
TST = transpose(matrix(l[3]))*transpose(matrix(l[2])); // 2nd term
size(ideal(TST));
==> 0
TST = transpose(matrix(l[2]))*transpose(matrix(l[1])); // 1st term
size(ideal(TST));
==> 0

User manual for Singular version 4.3.2, 2023, generated by texi2html.