|
|
5.1.94 modulo
Syntax:
modulo ( ideal_expression, ideal_expression )
modulo ( module_expression, module_expression )
modulo ( ideal_expression, ideal_expression{,} string_expression )
modulo ( module_expression, module_expression{,} string_expression )
modulo ( ideal_expression, ideal_expression{,} matrix_name )
Type:
- module
Purpose:
modulo(h1,h2)
represents
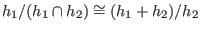 where where
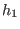 and and 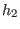 are considered as submodules of the same free module are considered as submodules of the same free module
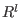 (l=1 for ideals). Let (l=1 for ideals). Let
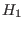 , resp. , resp. 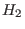 ,be the matrices of size ,be the matrices of size 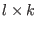 , resp. , resp. 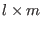 , having the
generators of , having the
generators of 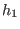 , resp. , resp. 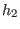 ,as columns.
Then ,as columns.
Then
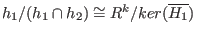 where where
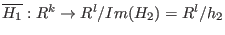 is the induced map.
is the induced map.
modulo(h1,h2) returns generators of
the kernel of this induced map.
An optional third string argument give the GB algorithm to use.
(default: "std", else: "groebner", "modstd", "slimgb").
An optional third argument (a name of a matrix) gives the matrix to store
the transformation of the input to the GB (see liftstd).
Note:
- If for at least one of
h1 or h2 the attribute "isHomog" is
set, modulo(h1,h2) also sets the attribute "isHomog"
(if possible, that is, if the weights are compatible).
Example:
| | ring r;
ideal h1=x,y,z;
ideal h2=x;
module m=modulo(h1,h2);
print(m);
==> 1,0, 0,0,
==> 0,-z,x,0,
==> 0,y, 0,x
|
See
hom_kernel;
syz.
|





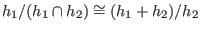 where
where
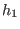 and
and 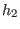 are considered as submodules of the same free module
are considered as submodules of the same free module
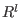 (l=1 for ideals). Let
(l=1 for ideals). Let
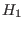 , resp.
, resp. 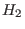 ,be the matrices of size
,be the matrices of size 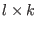 , resp.
, resp. 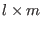 , having the
generators of
, having the
generators of 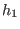 , resp.
, resp. 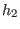 ,as columns.
Then
,as columns.
Then
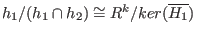 where
where
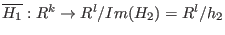 is the induced map.
is the induced map.