Singular Manual: chebyshev

D.4.6.4 chebyshev

Procedure from library decomp.lib (see decomp_lib).

Usage:

chebyshev(n); n int, n >= 0
chebyshev(n,c); n int, n >= 0, c number, c!=0

Return:

poly, the [monic] nth Chebyshev polynomial of the first kind.
The polynomials are defined in the first variable, say x, of the basering.

Note:

The (generalized) Chebyshev polynomials of the first kind can be defined by the recursion: $C_0 = c,\ C_1 = x,\ C_n = 2/c\cdot x\cdot C_{n-1}-C_{n-2},\ n \geq 2,c\neq 0$ .

These polynomials commute by composition:

$C_m \circ C_n = C_n\circ C_m$ .
For c=1, we obtain the standard (non monic) Chebyshev polynomials

which satisfy $T_n(x) = \cos(n \cdot \arccos(x))$ .
For c=2 (default), we obtain the monic Chebyshev polynomials

which satisfy the relation .
By default the monic Chebyshev polynomials are returned:

chebyshev(n) and chebyshev(n,1).
It holds $P_n(x) = 2\cdot T_n(x/2)$ and more generally

$C_n(c\cdot x) = c\cdot T_n(x)$
That is subst(chebyshev(n,c),var(1),c*var(1))= c*chebyshev(n,1).

If char(basering) = 2, then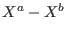

, and so on.

Example:

LIB "decomp.lib";
ring r = 0,x,lp;
// The monic Chebyshev polynomials
chebyshev(0);
==> 2
chebyshev(1);
==> x
chebyshev(2);
==> x2-2
chebyshev(3);
==> x3-3x
// These polynomials commute
compose(chebyshev(2),chebyshev(6)) ==
compose(chebyshev(6),chebyshev(2));
==> 1
// The standard Chebyshev polynomials
chebyshev(0,1);
==> 1
chebyshev(1,1);
==> x
chebyshev(2,1);
==> 2x2-1
chebyshev(3,1);
==> 4x3-3x
// -----------------------------------------------------------------------
// The relation for the various Chebyshev polynomials
5*chebyshev(3,1)==subst(chebyshev(3,5),x,5x);
==> 1
// -----------------------------------------------------------------------
// char 2 case
ring r2 = 2,x,dp;
chebyshev(2);
==> 1
chebyshev(3);
==> x

User manual for Singular version 4.4.0, 2024, generated by texi2html.