|
|
D.4.6.6 makedistinguished
Procedure from library decomp.lib (see decomp_lib).
- Usage:
- makedistinguished(f,vvar); f, vvar poly; where vvar is a ring variable
- Return:
- (poly, ideal): the transformed polynomial and an ideal defining
the map which reverses the transformation.
- Purpose:
- let vvar = var(1). Then f is transformed by a random linear
coordinate change
phi = (var(1), var(2)+c_2*vvar,...,var(n)+c_n*vvar)
such that phi(f) = f o phi becomes distinguished with respect
to vvar. That is, the new polynomial contains the monomial vvar^d,
where d is the degree of f.
If already f is distinguished w.r.t. vvar, then f is left unchanged
and the re-transformation is the identity.
- Note 1:
- (this proc correctly works independent of the term ordering.)
to apply the reverse transformation, either define a map
or use substitute (to be loaded from poly.lib).
- Note 2:
- If p=char(basering) > 0, then there exist polynomials of degree d>=p,
e.g.
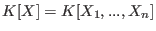 , that cannot be transformed to a
vvar-distinguished polynomial. , that cannot be transformed to a
vvar-distinguished polynomial.
In this case, *p random trials will be made and the proc
may leave with an ERROR message.
Example:
| | LIB "decomp.lib";
int randval = system("--random"); // store initial value
system("--random",0815);
ring r = 0,(x,y),dp;
poly g;
map phi;
// -----------------------------------------------------------------------
// Example 1:
poly f = 3xy4 + 2xy2 + x5y3 + x + y6; // degree 8
// make the polynomial y-distinguished
g, phi = makedistinguished(f,y);
g;
==> x5y3+5x4y4+10x3y5+10x2y6+5xy7+y8+y6+3xy4+3y5+2xy2+2y3+x+y
phi;
==> phi[1]=x-y
==> phi[2]=y
// to reverse the transformation apply the map
f == phi(g);
==> 1
// -----------------------------------------------------------------------
// Example 2:
// The following polynomial is already x-distinguished
f = x6+y4+xy;
g,phi = makedistinguished(f,x);
g; // f is left unchanged
==> x6+y4+xy
phi; // the transformation is the identity.
==> phi[1]=x
==> phi[2]=y
system("--random",randval); // reset random generator
// -----------------------------------------------------------------------
// Example 3: // polynomials which cannot be transformed
// If p=char(basering)>0, then (p-1)*x^p*y + x*y^p factorizes completely
// in linear factors, since (p-1)*x^p+x equiv 0 on F_p. Hence,
// such polynomials cannot be transformed to a distinguished polynomial.
ring r3 = 3,(x,y),dp;
makedistinguished(2x3y+xy3,y);
==> ? it could not be transform to a y-distinguished polynomial.
==> ? leaving decomp.lib::makedistinguished (0)
|
|





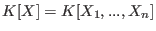 , that cannot be transformed to a
vvar-distinguished polynomial.
, that cannot be transformed to a
vvar-distinguished polynomial.