| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
D.4.25.3 normalToricRingFromBinomials
Procedure from librarynormaliz.lib (see normaliz_lib).
- Usage:
- normalToricRingFromBinomials(ideal I);
normalToricRingFromBinomials(ideal I, intvec grading); - Return:
- The ideal
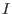 is generated by binomials of type
is generated by binomials of type 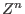 (multiindex notation)
in the surrounding polynomial ring
(multiindex notation)
in the surrounding polynomial ring
![$K[X]=K[X_1,...,X_n]$](sing_1019.png) . The binomials
represent a congruence on the monoid
. The binomials
represent a congruence on the monoid 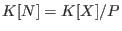 with residue monoid
with residue monoid 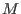 .
Let
.
Let  be the image of
be the image of 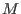 in gp(
in gp(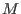 )/torsion. Then
)/torsion. Then  is universal in the
sense that every homomorphism from
is universal in the
sense that every homomorphism from 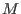 to an affine monoid factors through
to an affine monoid factors through  .
If
.
If 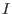 is a prime ideal, then
is a prime ideal, then ![$K[N]= K[X]/I$](sing_1021.png) . In general,
. In general, ![$K[N]=K[X]/P$](sing_1022.png) where
where
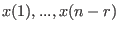 is the unique minimal prime ideal of
is the unique minimal prime ideal of 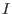 generated by binomials of type
generated by binomials of type
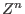 .
.
The function computes the normalization of
![$K[N]$](sing_1024.png) and returns a newly created
polynomial ring of the same Krull dimension, whose variables are
and returns a newly created
polynomial ring of the same Krull dimension, whose variables are
 , where
, where  is the rank of the matrix with rows
is the rank of the matrix with rows  .
(In general there is no canonical choice for such an embedding.)
Inside this polynomial ring there is an ideal
.
(In general there is no canonical choice for such an embedding.)
Inside this polynomial ring there is an ideal 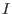 which lists the algebra
generators of the normalization of
which lists the algebra
generators of the normalization of ![$K[N]$](sing_1024.png) .
.
The function returns the input ideal I if an option blocking the computation of Hilbert bases has been activated.
However, in this case some numerical invariants are computed, and some other data may be contained in files that you can read into Singular (see showNuminvs, exportNuminvs).
LIB "normaliz.lib"; ring R = 37,(u,v,w,x,y,z),dp; ideal I = u2v-xyz, ux2-wyz, uvw-y2z; def S = normalToricRingFromBinomials(I); setring S; I; ==> I[1]=x(3) ==> I[2]=x(1) ==> I[3]=x(2)*x(3)^3 ==> I[4]=x(1)*x(2)*x(3)^2 ==> I[5]=x(1)^2*x(2)*x(3) ==> I[6]=x(1)^3*x(2) ==> I[7]=x(1)*x(2)^2*x(3)^4 ==> I[8]=x(1)^2*x(2)^2*x(3)^3 ==> I[9]=x(1)^2*x(2)^3*x(3)^5 |