| |
 |
 |
 |
 |
 |
 |
 |
 |
 |
7.4.1 G-algebras
Definition (PBW basis)
LetDefinition (G-algebra)
Let
![]() ,
where
,
where
![]() .
.
![]() is called a
is called a ![]() -algebra, if the following conditions hold:
-algebra, if the following conditions hold:
-
there is a monomial well-ordering
 on
on
![$K[x_1,x_2,\ldots,x_n]$](sing_229.png) such that
such that
 ,
, - non-degeneracy conditions:
 , where
, where

Note: Note that non-degeneracy conditions ensure associativity of multiplication,
defined by the relations. It is also proved, that they are necessary and sufficient to
guarantee the PBW property of an algebra, defined via C_ij and D_ij as above.
Theorem (properties of G-algebras)
Let ![]() be a
be a ![]() -algebra. Then
-algebra. Then
-
 has a PBW (Poincaré-Birkhoff-Witt) basis,
has a PBW (Poincaré-Birkhoff-Witt) basis, -
 is left and right noetherian,
is left and right noetherian, -
 is an integral domain.
is an integral domain.
Setting up a G-algebra
In order to set up a ![]() -algebra one has to do the following steps:
-algebra one has to do the following steps:
-
- define a commutative ring
![$R= K[x_1, \ldots, x_n]$](sing_233.png) , equipped with a monomial ordering
, equipped with a monomial ordering
 (see ring declarations (plural)).
(see ring declarations (plural)).
This provides us with the information on a field (together with its parameters), variables
(together with its parameters), variables
 and an ordering <.
and an ordering <.
From the sequence of variables we will build a G-algebra with the Poincaré-Birkhoff-Witt (PBW) basis .
. -
- define strictly
 upper triangular matrices (of type
upper triangular matrices (of type matrix)-
 , with nonzero entries
, with nonzero entries  of type number (
of type number ( for
for  will be ignored).
will be ignored). -
 , with polynomial entries
, with polynomial entries  from
from 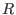 (
( for
for  will be ignored).
will be ignored).
-
-
- Call the initialization function
nc_algebra(C,D)(see nc_algebra) with the data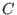 and
and  .
.
PLURAL does not check automatically whether the non-degeneracy conditions hold but it provides a procedure ndcond from the library nctools_lib to check this.