1.2 Examples for monomial orderings

Important orderings for applications are:

• The lexicographical ordering lp, given by the matrix:
  
  $$\left(\begin{array}{cccc} 1 & & &\\ & 1 & & 0\\ & & \ddots & \\ & 0 & & 1\end{array}\right)$$
  
  

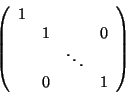
  resp. ls:
  

  $$\left(\begin{array}{cccc} -1 & & & \\ & -1 & & 0\\ & & \ddots &\\ & 0 & & -1\end{array}\right)$$
  
  
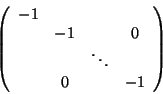
  Remark 1..1   The positive lexicraphic ordering lp on $K[x_1, \ldots, x_n]$ is an elimanation ordering for $x_1,\ldots,x_i\ \forall 1 \leq i \leq n$

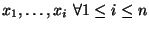
  The definition of rings with these orderings in SINGULAR:
  (Each line starting with // is a comment in SINGULAR.)

  ring R1=0,(x(1..5)),lp;
  ring R2=0,(x(1..5)),ls;
  

• The weighted degree reverse lexicographical ordering, given by the matrix
  
  $$wp: \left( \begin{array}{cccc} w_1 & w_2 & \ldots & w_n\\ & & & -1\\ & & \diagup & \\ 0 & -1 & & \end{array}\right)$$
  
  
  $w_i > 0 \forall i$, (resp. $ws: w_1 \neq 0, w_i \in {\rm\bf Z}\ \forall i$).

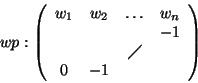
  If w_i = 1 (respectively w_i = -1) for all i we obtain the degree reverse lexicographical ordering, dp (respectively ds).

  The definition of rings with these orderings in SINGULAR:

  ring R3=0,(x(1..5)),wp(2,3,4,5,6);
  // correspond to w_i:2,3,4,5,6
  ring R4=0,(x(1..5)),ws(2,3,4,5,6);
  // correspond to w_i:-2,-3,-4,-5,-6
  ring R5=0,(x(1..4)),dp;
  ring R6=0,(x(1..4)),ds;
  

• An example for an elimination ordering for $x_{r+1}, \ldots, x_n$ in $K[\underline{x}] = \mbox{ Loc}_< K[\underline{x}]$ is given by the matrix
  
  $$\left( \begin{array}{cccccccc} 0 & 0 & \ldots & 0 & w_{r+1} ... ... & \diagup & & & & &\\ 0 & -1 & & & & & & \end{array}\right)$$
  
  
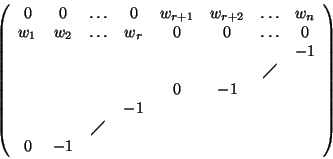
  with $w_1 > 0, \ldots, w_n > 0$. In $K[x_1, \ldots, x_r]_{(x_1, \ldots, x_r)} [x_{r+1}, \ldots, x_n] = \mbox{ Loc}_<K[\underline{x}]$ it is given by the same matrix with $w_1 < 0, \ldots, w_r < 0$ and $w_{r+1} > 0, \ldots, w_n > 0$.

  The definition of a polynomial ring with an elimination ordering for x₃ and x₄ in SINGULAR:

  ring E=0,(x(1..4)),(a(0,0,1,1),a(1,1),dp);
  // correspond to w_i=1 for all i, r=2
  // or simpler:
  ring EE=0,(x(1..4)),(a(0,0,1,1),dp);
  

• The product ordering, given by the matrix
  
  $$\left( \begin{array}{cccc} A_1 & & & 0\\ & A_2 & & \\ & & \ddots & \\ 0 & & &A_k \end{array}\right)$$
  
  
  if the A_i define orderings on monomials given by the corresponding subsets of $\{x_1, \ldots, x_n\}$. Such an ordering can be used to compute in
  • $K(\underline{y})[\underline{x}]$ ( $A_1: {\rm dp}\ on\ \underline{x},\ A_2: {\rm dp}\ on\ \underline{y}$)
  • $(K[\underline{y}]_{(\underline{y})})[\underline{x}]$ ( $A_1: {\rm dp}\ on\ \underline{x},\ A_2: {\rm ds}\ on\ \underline{y}$)
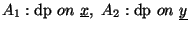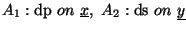  • $(K[\underline{y}])[\underline{x}]_{([\underline{x})}$ ( $A_1: {\rm ds}\ on\ \underline{x},\ A_2: {\rm dp}\ on\ \underline{y}$)
  (See [GTZ], [GG], definition 2.1).

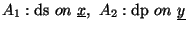  The definition of a ring with this ordering in SINGULAR:

  ring P=0,(x(1..6)),(dp(4),ds(2));
  // correspond to
  // a first block of 4 variables with ordering dp
  // and a second block of 2 variables with ordering ds