


Next: 2.3.2 Elimination
Up: 2.3 Basic properties
Previous: 2.3 Basic properties
Definition 2..5
A function
![$NF : K[\underline{x}]^r \times \{G \vert G\ standard basis\} \to K[\underline{x}]^r, (p,G) \mapsto NF(p\vert G)$](img70.gif)
,
is called a
normal form
if for any
![$p \in K[\underline{x}]^r$](img71.gif)
and any
G the following holds: if
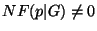
then
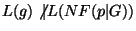
for all
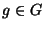
.
NF(
g|
G) is called
the
normal form of 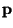 with respect to
with respect to 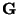
.
Lemma 2..6
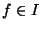
iff
NF(
f,
std(
I)) = 0.
SINGULAR example:
//f defines a trimodal singularity for generic moduli
ring R = 0,(x,y),ds;
int a1,a2,a3=random(1,100),random(-100,1),random(1,100);
poly f = (x^2-y^3)*(y+a1*x)*(y+a2*x)*(y+a3*x);
ideal J = jacob(f);
ideal I = f;
// J:I, ideal of the closure of V(J) \ V(I)
ideal Q = quotient(J,I);
//the Hessian of f
poly Hess = det(jacob(jacob(f)));
//Hess is contained in Q iff NF is 0
reduce(Hess,std(Q));
| ZCA Home |
Reports |