


Next: Bibliography
Up: Relating Rewriting Techniques on
Previous: 6. Relating the Submonoid
The class of finitely presented groups contains subclasses which -
using appropriate presentations - allow to solve the subgroup problem
using string rewriting techniques.
In this paper we have pointed out how these results are related to the
existence (and in fact even the construction) of Gröbner bases
in the respective group rings.
This shall now be summarized in the following table, which lists the
reductions which - again using appropriate presentations for the groups -
ensure the construction of the respective finite Gröbner basis of ideals.
Note that
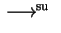 stands for suffix,
stands for suffix,
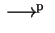 for
prefix,
for
prefix,
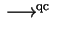 for
quasi-commutative,
for
quasi-commutative,
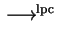 for left-polycyclic reduction
and
for left-polycyclic reduction
and
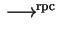 for right-polycyclic reduction
(for more information on the reductions and the computation of
Gröbner bases related to them see [MaRe93,Re95,MaRe95,MaRe97,Re96,MaRe96]).
for right-polycyclic reduction
(for more information on the reductions and the computation of
Gröbner bases related to them see [MaRe93,Re95,MaRe95,MaRe97,Re96,MaRe96]).
| Group |
left ideals |
right ideals |
two-sided ideals |
|---|
| free |
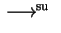 |
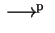 |
none7 |
| plain |
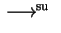 |
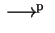 |
none |
| context-free |
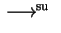 |
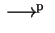 |
none |
| nilpotent |
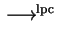 |
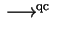 |
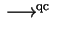 |
| |
|
|
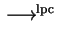 |
| polycyclic |
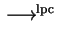 |
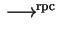 |
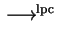 |
| |
|
|
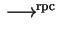 |
As mentioned above, the different reductions require special forms of
presentations for the respective groups.
Free groups need free presentations with length-lexicographical
completion ordering for prefix and suffix reduction.
Plain groups require canonical 2-monadic presentations with inverses
of length 1 and again length-lexicographical completion ordering
for prefix as well as suffix reduction.
Context-free groups demand virtually free presentations (see [CrOt94])
for prefix and a modified version of these presentations for suffix reduction.
All these special forms of the presentations are similarly required
when solving the subgroup problem using prefix rewriting techniques.
For nilpotent groups we need convergent PCNI-systems
for quasi-commutative and left-polycyclic reduction.
In the case of polycyclic groups we need PCP-systems
for left-polycyclic and reversed PCP-systems for
right-polycyclic reduction.



Next: Bibliography
Up: Relating Rewriting Techniques on
Previous: 6. Relating the Submonoid
| ZCA Home |
Reports |