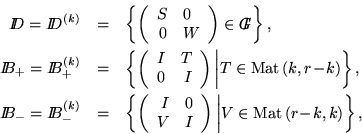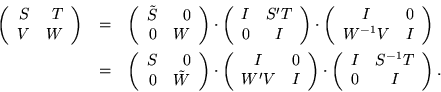Next: 3. Row-minimal matrices
Up: Splitting algorithm for vector
Previous: 1. Introduction and notation
2. Block type Bruhat decomposition
For the convenience of the reader, we include some elementary,
well-known facts from linear algebra which we shall need.
(2.1)
Fix an integer
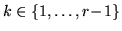 and let
and let
After a permutation of rows (or columns), any regular matrix will
belong to
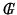 .
.
Consider the following subgroups of Glr contained in
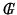 :
:
where I always denotes the unit matrix of the corresponding size.
(2.2)
The following lema will be verified by direct computation:
Here 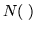 denotes the normalizer in Glr(R).
denotes the normalizer in Glr(R).
(i1)
Just check the following identities:
(i2)
From the identity
assuming that the first matrix is in
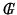 ,
we obtain
T'=-S-1 T W' and
V'=-W-1VS'; hence,
SS'-TW-1 VS'=I. Thus, S' is
invertible and
,
we obtain
T'=-S-1 T W' and
V'=-W-1VS'; hence,
SS'-TW-1 VS'=I. Thus, S' is
invertible and
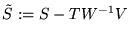 is its inverse.
Similarly,
is its inverse.
Similarly,
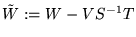 is the inverse of W' .
is the inverse of W' .
(i3)
Using the notation of (i2) we obtain
(2.3)
Fix a k-subset J of row indices
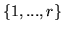 .
Let QJ be the submatrix
of Q formed by those rows of Q whose index belongs to J.
Then
.
Let QJ be the submatrix
of Q formed by those rows of Q whose index belongs to J.
Then
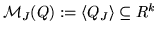 is invariant under equivalence
of matrices. After a certain permutation of rows of Q, it is enough to consider
for simplicity only the special cases
is invariant under equivalence
of matrices. After a certain permutation of rows of Q, it is enough to consider
for simplicity only the special cases
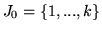 ,
,
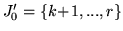



Next: 3. Row-minimal matrices
Up: Splitting algorithm for vector
Previous: 1. Introduction and notation
| ZCA Home |
Reports |