


Next: 1 monomial operations
Up: Monomial Representations for Gröbner Computations
Previous: 1 Introduction
2 Basic monomial operations and representations
Given an integer n > 0 we define the set of exponent vectors Mn
by
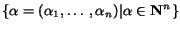 .
Notice that monomials usually denote terms of the form
.
Notice that monomials usually denote terms of the form
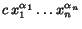 .
However, in this paper we do
only consider the exponent vector of a monomial and shall therefore
use the words exponent vector and monomial interchangeably (i.e., we
identify a monomial with its exponent vector).
.
However, in this paper we do
only consider the exponent vector of a monomial and shall therefore
use the words exponent vector and monomial interchangeably (i.e., we
identify a monomial with its exponent vector).
We furthermore use Greek letters to denote monomials and the letter
n to denote the a-priory given length of monomials (which is the
number of variables in the corresponding polynomial ring).
Monomials play a central role in GB computations. In this section, we
describe the basic monomial operations and discuss basic facts about
monomial (resp. polynomial) representations for GB computations.



Next: 1 monomial operations
Up: Monomial Representations for Gröbner Computations
Previous: 1 Introduction
| ZCA Home |
Reports |