


Next: 3. The Subgroup Problem
Up: Observations on Coset Enumeration
Previous: 1. Introduction
2. String Rewriting Methods
First we give some basic definitions for string rewriting systems
(for a general reference of the terms and techniques described here see
[2]).
A string rewriting system
T over a finite alphabet 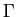 is a subset of
is a subset of
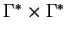 .
The elements
.
The elements
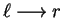 of T are called
rules.
The single-step reduction relation
on
of T are called
rules.
The single-step reduction relation
on 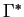 induced
by T is defined as follows:
For any u,v in
induced
by T is defined as follows:
For any u,v in 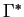 ,
,
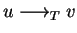 if and only if there exist
x,y in
if and only if there exist
x,y in 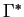 and
and
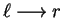 in T such that
in T such that
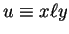 and
and
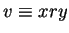 .
v is then called a proper descendant of u.
The reflexive transitive symmetric closure is
denoted by
.
v is then called a proper descendant of u.
The reflexive transitive symmetric closure is
denoted by
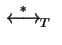 .
If
.
If
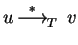 holds then one says that u reduces to v.
In case u has no proper descendant u is called irreducible.
An irreducible descendant of u is called a T-normal form.
Such normal forms need neither exist nor be unique.
The reduction relation
holds then one says that u reduces to v.
In case u has no proper descendant u is called irreducible.
An irreducible descendant of u is called a T-normal form.
Such normal forms need neither exist nor be unique.
The reduction relation
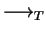 is called Noetherian or terminating
if and only if there is no
infinite chain
is called Noetherian or terminating
if and only if there is no
infinite chain
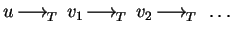 .
In this case normal forms always exist.
It is called confluent if for all u,v,w in
.
In this case normal forms always exist.
It is called confluent if for all u,v,w in 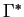 ,
,
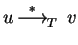 and
and
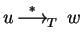 imply the existence of z in
imply the existence of z in 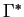 such that
such that
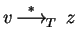 and
and
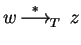 .
Then normal forms are unique in case they exist.
A string rewriting system is called convergent or complete if it is both,
Noetherian and confluent, i.e., unique normal forms exist.
By Newman's lemma we know that under the hypothesis that a
reduction relation is Noetherian, a string rewriting system is confluent if
and only if it is locally confluent, i.e., for all u,v,w in
.
Then normal forms are unique in case they exist.
A string rewriting system is called convergent or complete if it is both,
Noetherian and confluent, i.e., unique normal forms exist.
By Newman's lemma we know that under the hypothesis that a
reduction relation is Noetherian, a string rewriting system is confluent if
and only if it is locally confluent, i.e., for all u,v,w in 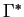 ,
,
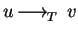 and
and
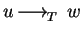 imply the existence of
z in
imply the existence of
z in 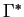 such that
such that
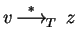 and
and
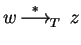 .
For finite string rewriting systems the global property of being locally
confluent can be localized to enable a finite confluence test by standard critical pair sets.
The process of trying to turn a Noetherian string rewriting system into a
convergent one by resolving the not locally confluent situations is
called completion and is performed by
the Knuth-Bendix completion procedure (abbreviated by KB)
which is based on resolving critical pairs.
Since the word problem for string rewriting systems is undecidable,
such a completion procedure
in general will not terminate.
Nevertheless, using a fair3 strategy, it
always enumerates a convergent string rewriting system presenting the same
monoid as the input system.
.
For finite string rewriting systems the global property of being locally
confluent can be localized to enable a finite confluence test by standard critical pair sets.
The process of trying to turn a Noetherian string rewriting system into a
convergent one by resolving the not locally confluent situations is
called completion and is performed by
the Knuth-Bendix completion procedure (abbreviated by KB)
which is based on resolving critical pairs.
Since the word problem for string rewriting systems is undecidable,
such a completion procedure
in general will not terminate.
Nevertheless, using a fair3 strategy, it
always enumerates a convergent string rewriting system presenting the same
monoid as the input system.
Henceforth in this paper, we will only consider string rewriting systems
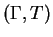 such that for
such that for
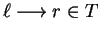 we have
we have 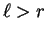 for some well-founded admissible ordering > on
for some well-founded admissible ordering > on
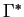 .
This ordering will be the length-lexicographic in the examples given here.
.
This ordering will be the length-lexicographic in the examples given here.
Now any group presentation in terms of generators 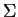 and relators R gives rise to
a string rewriting system by setting
and relators R gives rise to
a string rewriting system by setting
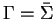 and
and
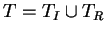 where
where
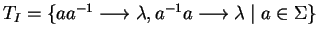 and
and
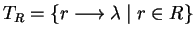 .
Running KB on this input results in a (possibly infinite) completion
of the presentation with respect to the chosen completion ordering on
.
Running KB on this input results in a (possibly infinite) completion
of the presentation with respect to the chosen completion ordering on
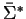 .
If the resulting convergent system is finite many questions concerning the group can
be answered (see e.g. [2]).
.
If the resulting convergent system is finite many questions concerning the group can
be answered (see e.g. [2]).
Another specialized string rewriting technique used to study subgroups of groups is
prefix string rewriting.
Any string rewriting system
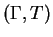 can be interpreted as a prefix string rewriting
system with a single-step reduction relation on
can be interpreted as a prefix string rewriting
system with a single-step reduction relation on 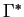 induced by T as follows:
For any u,v in
induced by T as follows:
For any u,v in 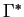 ,
,
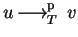 if and only if there exist
y in
if and only if there exist
y in 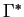 and
and
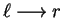 in T such that
in T such that
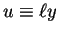 and
and
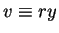 .
The notions irreducible, T-normal form, Noetherian, confluent and convergent with respect
to prefix string rewriting carry over naturally.
A completion procedure with respect to prefix string rewriting is nothing else than
an interreduction of the respective set of rules by prefix rewriting
and in contrary to KB always
terminates for the finite string rewriting systems we are looking at in this paper.
.
The notions irreducible, T-normal form, Noetherian, confluent and convergent with respect
to prefix string rewriting carry over naturally.
A completion procedure with respect to prefix string rewriting is nothing else than
an interreduction of the respective set of rules by prefix rewriting
and in contrary to KB always
terminates for the finite string rewriting systems we are looking at in this paper.



Next: 3. The Subgroup Problem
Up: Observations on Coset Enumeration
Previous: 1. Introduction
| ZCA Home |
Reports |
![]() such that for
such that for
![]() we have
we have ![]() for some well-founded admissible ordering > on
for some well-founded admissible ordering > on
![]() .
This ordering will be the length-lexicographic in the examples given here.
.
This ordering will be the length-lexicographic in the examples given here.
![]() and relators R gives rise to
a string rewriting system by setting
and relators R gives rise to
a string rewriting system by setting
![]() and
and
![]() where
where
![]() and
and
![]() .
Running KB on this input results in a (possibly infinite) completion
of the presentation with respect to the chosen completion ordering on
.
Running KB on this input results in a (possibly infinite) completion
of the presentation with respect to the chosen completion ordering on
![]() .
If the resulting convergent system is finite many questions concerning the group can
be answered (see e.g. [2]).
.
If the resulting convergent system is finite many questions concerning the group can
be answered (see e.g. [2]).
![]() can be interpreted as a prefix string rewriting
system with a single-step reduction relation on
can be interpreted as a prefix string rewriting
system with a single-step reduction relation on ![]() induced by T as follows:
For any u,v in
induced by T as follows:
For any u,v in ![]() ,
,
![]() if and only if there exist
y in
if and only if there exist
y in ![]() and
and
![]() in T such that
in T such that
![]() and
and
![]() .
The notions irreducible, T-normal form, Noetherian, confluent and convergent with respect
to prefix string rewriting carry over naturally.
A completion procedure with respect to prefix string rewriting is nothing else than
an interreduction of the respective set of rules by prefix rewriting
and in contrary to KB always
terminates for the finite string rewriting systems we are looking at in this paper.
.
The notions irreducible, T-normal form, Noetherian, confluent and convergent with respect
to prefix string rewriting carry over naturally.
A completion procedure with respect to prefix string rewriting is nothing else than
an interreduction of the respective set of rules by prefix rewriting
and in contrary to KB always
terminates for the finite string rewriting systems we are looking at in this paper.