


Next: 6. Sims' Approach
Up: Observations on Coset Enumeration
Previous: 4. The Todd-Coxeter Coset
5. Kuhn and Madlener's Approach
In [4] a procedure for completing the reduction relation
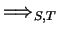 as described
in Section 3 is
provided for the case that the group presentation
as described
in Section 3 is
provided for the case that the group presentation
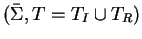 is convergent.
The basic idea is to interpret the rules defining the group as the (possibly infinite)
set of prefix string rewriting rules
is convergent.
The basic idea is to interpret the rules defining the group as the (possibly infinite)
set of prefix string rewriting rules
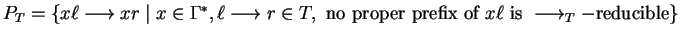 .
Then
.
Then
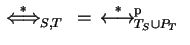 .
A completion procedure for this reduction relation has TS and T as input and on termination
a set TC as output which is constructed as follows:
TC is initialized as TS.
The completion step then
considers critical situations between rules
.
A completion procedure for this reduction relation has TS and T as input and on termination
a set TC as output which is constructed as follows:
TC is initialized as TS.
The completion step then
considers critical situations between rules
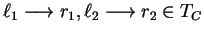 of the form
of the form
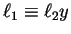 or
between rules
or
between rules
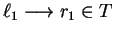 and
and
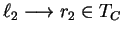 of the form
of the form
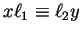 with
with
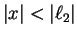 .
The overlaps between rules in T can be omitted as T is already convergent.
If critical situations cannot be resolved, the newly arising rules are added to TC.
On termination the (still possibly infinite) set
.
The overlaps between rules in T can be omitted as T is already convergent.
If critical situations cannot be resolved, the newly arising rules are added to TC.
On termination the (still possibly infinite) set
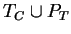 is convergent as
a prefix string rewriting system.
It is known that for subgroups of finite index the procedure terminates.
In this case the interreduced version of the set
is convergent as
a prefix string rewriting system.
It is known that for subgroups of finite index the procedure terminates.
In this case the interreduced version of the set
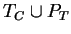 is finite and
corresponds to the set RTC arising from the coset table for TC as described in the
previous section.
Of course in order to treat Example 2 we have to use a convergent group presentation
for
is finite and
corresponds to the set RTC arising from the coset table for TC as described in the
previous section.
Of course in order to treat Example 2 we have to use a convergent group presentation
for 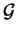 instead of the defining relators presented in the previous section.
Completing
instead of the defining relators presented in the previous section.
Completing
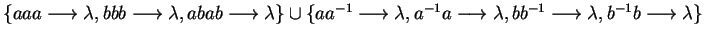 with
respect to the length-lexicographical ordering induced by the precedence
with
respect to the length-lexicographical ordering induced by the precedence
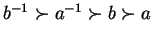 gives us the convergent string rewriting system
gives us the convergent string rewriting system
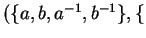
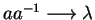 ,
,
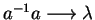 ,
,
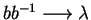 ,
,
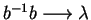 ,
,
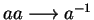 ,
,
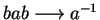 ,
,
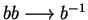 ,
,
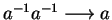 ,
,
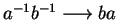 ,
,
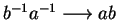 ,
,
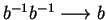 ,
,
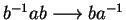 ,
,
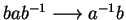 ,
,
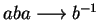 ,
,
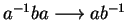 ,
,
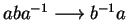 ,
,
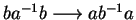 ,
,
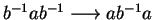 ,
,
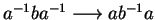
 and on input
and on input
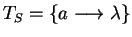 on termination we get the set
on termination we get the set
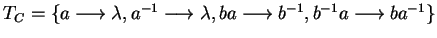 and the convergent prefix string rewriting system
and the convergent prefix string rewriting system
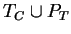 can be prefix interreduced to the set of rules RTC in Example 2.
can be prefix interreduced to the set of rules RTC in Example 2.
While sometimes also successful for subgroups of infinite index,
this method is no longer applicable to groups given by arbitrary presentations.
This would also require that on completing TC we additionally have to resolve critical
situations arising from overlaps of rules in T.
This is essentially what happens in Sims' approach.



Next: 6. Sims' Approach
Up: Observations on Coset Enumeration
Previous: 4. The Todd-Coxeter Coset
| ZCA Home |
Reports |