| Ordering |
Precedence on 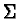 |
| kbo-A |
(a 1)  (c 1) (c 1)  (c 1) (c 1)  (A 6) (A 6)  (B 1) (B 1)  (C 1) (C 1) |
| kbo-B |
(a 1)  (b 1) (b 1)  (c 1) (c 1)  (A 1) (A 1)  (B 6) (B 6)  (C 1) (C 1) |
| kbo-C |
(a 1)  (b 1) (b 1)  (c 1) (c 1)  (A 1) (A 1)  (B 1) (B 1)  (C 6) (C 6) |
| kbo-a |
(a 6)  (b 1) (b 1)  (c 1) (c 1)  (A 1) (A 1)  (B 1) (B 1)  (C 1) (C 1) |
| kbo-b |
(a 1)  (b 6) (b 6)  (c 1) (c 1)  (A 1) (A 1)  (B 1) (B 1)  (C 1) (C 1) |
| kbo-c |
(a 1)  (b 1) (b 1)  (c 6) (c 6)  (A 1) (A 1)  (B 1) (B 1)  (C 1) (C 1) |
| ll-CcBbAa |
C  c c  B B  b b  A A  a a |
| syl-l-bBaAcC |
b  B B  a a  A A  c c  C C |
| syl-r-bBaAcC |
b  B B  a a  A A  c c  C C |