


Next: 3.2 Regular Extensions
Up: 3. The Extension of
Previous: 3. The Extension of
3.1 Criteria for Regularity
In the case of a graded ring 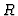 and a graded ideal
and a graded ideal 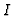 we obtain a first
necessary und sufficient condition for the regularity
of
we obtain a first
necessary und sufficient condition for the regularity
of 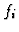 over
over 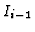 using on the computation of Hilbert series.
using on the computation of Hilbert series.
Consider the exact sequence
where the left most mapping is the multiplication by the class of 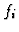 in
in
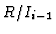 . We denote this mapping by
. We denote this mapping by 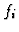 , too. Assume that
, too. Assume that 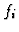 is regular over
is regular over 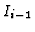 , i.e.,
, i.e., 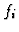 is not a zero divisor in
is not a zero divisor in 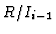 .
Then the mapping
.
Then the mapping 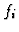 is a monomorphism and the Hilbert series of
is a monomorphism and the Hilbert series of
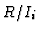 is the difference of those of
is the difference of those of 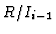 and
and
![$(R/I_{i-1})[deg(f_i)]$](img19.gif) ,
where
,
where
![$(R/I_{i-1})[deg(f_i)]$](img19.gif) denotes the module
denotes the module 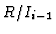 with the degree
shifted by
with the degree
shifted by 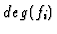 . If
. If 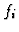 is not regular the Hilbert series of
is not regular the Hilbert series of
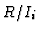 is different from this difference. Hence, the knowledge of the standard
base of
is different from this difference. Hence, the knowledge of the standard
base of 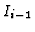 and
and 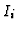 provide us with a criterion for the regularity of
provide us with a criterion for the regularity of
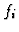 .
.
Let 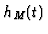 denote the Hilbert serie of the
denote the Hilbert serie of the 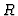 -module
-module 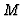 .
.
Lemma 3.2
The element
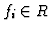
is
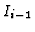
-regular if and only if
There is a second, simple, but, nevertheless very usefull criterion (not
assuming gradedness).
Lemma 3.3
The element
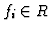
is
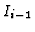
-regular if and only if
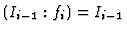
.
PROOF: We have
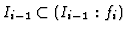 . If
. If 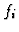 is not a zero divisor
over
is not a zero divisor
over 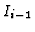 then any element of
then any element of 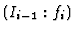 lies in
lies in 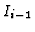 .
.
Consider the module
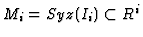 of all syzygies of
of all syzygies of 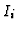 .
Then the
.
Then the 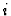 -th component of
-th component of 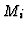 represents the relative syzygies of
represents the relative syzygies of
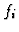 over
over 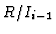 . The ideal generated by the
. The ideal generated by the 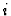 -th component
of
-th component
of 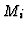 is just
is just 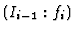 .
.
Definition 3.4
We define
and call
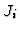
the
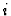
-th extension ideal of
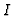
with respect to the
sequence
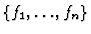
.



Next: 3.2 Regular Extensions
Up: 3. The Extension of
Previous: 3. The Extension of
| ZCA Home |
Reports |
![]() denote the Hilbert serie of the
denote the Hilbert serie of the ![]() -module
-module ![]() .
.