5. Singularities and standard bases

A (complex) singularity is, by definition, nothing but a complex analytic germ $(V,0)$ together with its analytic local ring $R = {\mathbb{C}}\{x\}/I$, where ${\mathbb{C}}\{x\}$ is the convergent power series ring in $x = x_1, \dots, x_n$. For an arbitrary field $K$ let $R = K[[x]] /I$ for some ideal $I$ in the formal power series ring $K[[x]]$. We call $(V,0) = ($Spec$\,R, \mathfrak{m})$ or just $R$ a singularity ( $\mathfrak{m}$ denotes the maximal ideal of the local ring $R$) and write $K\langle x \rangle$ for the convergent and for the formal power series ring if the statements hold for both.

If $I \subset K[x]$ is an ideal with $I \subset \langle x \rangle = \langle x_1, \dots, x_n\rangle$ then the singularity of $V(I)$ at $0 \in K^n$ is, using the above notation, $K \langle x\rangle /I \cdot K\langle x\rangle$. However, we may also consider the local ring $K[x]_{\langle x \rangle}/I \cdot K[x]_{\langle x \rangle}$ with $K[x]_{\langle x\rangle}$ the localisation of $K[x]$ at $\langle x \rangle$, as the singularity of $V(I)$ at 0. Geometrically, for $K = {\mathbb{C}}$, the difference is the following: ${\mathbb{C}}\{x\}/I {\mathbb{C}}\{x\}$ describes the variety $V(I)$ in an arbitrary small neighbourhood of 0 in the Euclidean topology while ${\mathbb{C}}[x]_{\langle x \rangle}/I {\mathbb{C}}[x]_{\langle x \rangle}$ describes $V(I)$ in an arbitrary small neighbourhood of 0 in the (much coarser) Zariski topology.

At the moment, we can compute efficiently only in $K[x]_{\langle x\rangle}$ as we shall explain below. In many cases of interest, we are happy since invariants of $V(I)$ at 0 can be computed in $K[x]_{\langle x\rangle}$ as well as in $K\langle x \rangle$. There are, however, others (such as factorisation), which are completely different in both rings.

$(V,0)$ is called non-singular or regular or smooth if $K\langle x \rangle/I$ is isomorphic (as local ring) to a power series ring $K\langle y_1, \dots, y_d\rangle$, or if $K[x]_{\langle x \rangle}/I$ is a regular local ring.

By the implicit function theorem, or by the Jacobian criterion, this is equivalent to the fact that $I$ has a system of generators $g_1, \dots, g_{n-d}$ such that the Jacobian matrix of $g_1, \dots, g_{n-d}$ has rank $n-d$ in some neighbourhood of 0. $(V,0)$ is called an isolated singularity if there is a neighbourhood $W$ of 0 such that $W \cap (V \smallsetminus\{0\})$ is regular everywhere.

In order to compute with singularities, we need the notion of standard basis which is a generalisation of the notion of Gröbner basis, cf. GP1,GP2.

A monomial ordering is a total order on the set of monomials $\{x^\alpha \vert \alpha \in {\mathbb{N}}^n\}$ satisfying

$$x^\alpha > x^\beta \Rightarrow x^{\alpha + \gamma} > x^{\beta + \gamma}$$    for all $$\alpha, \beta, \gamma \in {\mathbb{N}}^n.$$

We call a monomial ordering $>$ global (resp. local, resp. mixed) if $x_i > 1$ for all $i$ (resp. $x_i< 1$ for all $i$, resp. if there exist $i,j$ so that $x_i< 1$ and $x_j > 1$). This notion is justified by the associated ring to be defined below. Note that $>$ is global if and only if $>$ is a well-ordering (which is usually assumed).

Any $f \in K[x]\smallsetminus\{0\}$ can be written uniquely as $f = cx^\alpha + f'$, with $c \in K\smallsetminus\{0\}$ and $\alpha > \alpha'$ for any non-zero term $c' x^{\alpha'}$ of $f'$. We set lm $(f) = x^\alpha$, the leading monomial of $f$ and lc$\,(f) = c$, the leading coefficient of $f$.

For a subset $G \subset K[x]$ we define the leading ideal of $G$ as

$$L(G) = \langle$$    lm$$(g) \;\vert\; g \in G\smallsetminus\{0\}\rangle_{K[x]},$$

the ideal generated by the leading monomials in $G\smallsetminus\{0\}$.

So far, the general case is not different to the case of a well-ordering. However, the following definition provides something new for non-global orderings:

For a monomial ordering $>$ define the multiplicatively closed set

$$S_> := \{u \in K[x]\smallsetminus\{0\}\;\vert\;$$lm$$\,(u) = 1\}$$

and the $K$-algebra

$$R:=$$   Loc$$\,K[x] := S^{-1}_> K[x] = \{\dfrac{f}{u} \;\vert\; f \in K[x], u \in S_>\},$$

the localisation (ring of fractions) of $K[x]$ with respect to $S_>$. We call Loc$\,K[x]$ also the ring associated to $K[x]$ and $>$.

Note that $K[x] \subset$   Loc$\,K[x] \subset K[x]_{\langle x\rangle}$ and Loc$\, K[x] = K[x]$ if and only if $>$ is global and Loc$\,K[x] = K[x]_{\langle x\rangle}$ if and only if $>$ is local (which justifies the names).

Let $>$ be a fixed monomial ordering. In order to have a short notation, I write

$$R:=$$   Loc$$\,K[x] = S^{-1}_> K[x]$$

to denote the localisation of $K[x]$ with respect to $>$.

Let $I \subset R$ be an ideal. A finite set $G \subset I$ is called a standard basis of $I$ if and only if $L(G) = L(I)$, that is, for any $f \in I\smallsetminus\{0\}$ there exists a $g \in G$ satisfying lm$\,(g)\vert$lm$\,(f)$.

If the ordering is a well-ordering, then a standard basis $G$ is called a Gröbner basis. In this case $R = K[x]$ and, hence, $G \subset I \subset K[x]$.

Standard bases can be computed in the same way as Gröbner bases except that we need a different normal form. This was first noticed by Mo for local orderings (called tangent cone orderings by Mora) and, in general, by GP1,Getal.

Let ${\mathcal G}$ denote the set of all finite and ordered subsets $G \subset R$. A map

   NF$$\,: R \times {\mathcal G}\to R,\; (f,G) \mapsto$$   NF$$\,(f\vert G),$$

is called a normal form on $R$ if, for all $f$ and $G$,

(i)

NF$\,(f\vert G) \not= 0 \Rightarrow$   lm$\,\bigl($NF$\,(f\vert G)\bigr) \not\in L(G)$,

(ii)

$f -$   NF$\,(f\vert G) \in \langle G\rangle_R$, the ideal in $R$ generated by $G$.

NF is called a weak normal form if, instead of (ii), only the following condition (ii') holds:

(ii')

for each $f \in R$ and each $G \in {\mathcal G}$ there exists a unit $u \in R$, so that $uf-$NF$\,(f\vert G) \in \langle G\rangle_R$.

Moreover, we need (in particular for computing syzygies) (weak) normal forms with standard representation: if $G = \{g_1, \dots, g_k\}$, we can write

$$f -$$   NF$$\,(f\vert G) = \sum^k_{i=1} a_i g_i,\quad a_i \in R,$$

such that lm$\,\bigl(f-$NF$\,(f\vert G)\bigr) \ge$   lm$\,(a_ig_i)$ for all $i$, that is, no cancellation of bigger leading terms occurs among the $a_i g_i$.

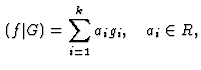
Indeed, if $f$ and $G$ consist of polynomials, we can compute, in finitely many steps, weak normal forms with standard representation such that $u$ and NF$\,(f\vert G)$ are polynomials and, hence, compute polynomial standard bases which enjoy most of the properties of Gröbner bases.

Once we have a weak normal form with standard representation, the general standard basis algorithm may be formalised as follows:

STANDARDBASIS(G,NF) [arbitrary monomial ordering]

Input: $G$ a finite and ordered set of polynomials, NF a weak normal form with standard representation.

Output: $S$ a finite set of polynomials which is a standard basis of $\langle G\rangle_R$.

- $S = G$;
- $P = \{(f,g) \mid f,g\in S\}$;
- while $(P \not= \emptyset)$
choose $(f,g) \in P$;
$P = P \smallsetminus \{(f,g)\}$;
$h =$   NF$\,($spoly$(f,g)\mid S)$;
if $(h \not= 0)$
$P = P \cup \{(h,f) \mid f \in S\}$;
$S = S \cup \{h\}$;
- return $S$;

Here spoly $(f,g) = x^{\gamma - \alpha} f - \tfrac{lc(f)}{lc(g)} x^{\gamma - \beta} g$ denotes the $\boldsymbol{s}$-polynomial of $f$ and $g$ where $x^\alpha =$   lm$\,(f),\; x^\beta =$   lm$\,(g),\; \gamma = lcm(\alpha,\beta)$.

The algorithm terminates by Dickson's lemma or by the noetherian property of the polynomial ring (and since NF terminates). It is correct by Buchberger's criterion, which generalises to non-well-orderings.

If we use Buchberger's normal form below, in the case of a well-ordering, STANDARDBASIS ist just Buchberger's algorithm:

NFBUCHBERGER(f,G) [well-ordering]

Input: $G$ a finite ordered set of polynomials, $f$ a polynomial.

Output: $h$ a normal form of $f$ with respect to $G$ with standard representation.

- $h = f$;
- while $(h \not= 0$ and exist $g \in G$ so that lm$\,(g)\mid$lm$\,(h))$
choose any such $g$;
$h =$   spoly$(h,g)$;
- return $h$;

For an algorithm to compute a weak normal form in the case of an arbitrary ordering, we refer to GP1.

To illustrate the difference between local and global orderings, we compute the dimension of a variety at a point and the (global) dimension of the variety.

The dimension of the singularity $(V,0)$, or the dimension of $V$ at 0, is, by definition, the Krull dimension of the analytic local ring ${\mathcal O}_{V,0} = K\langle x \rangle/I$, which is the same as the Krull dimension of the algebraic local ring $K[x]_{\langle x \rangle}/I$ in case $I = \langle f_1, \dots, f_k\rangle$ is generated by polynomials, which follows easily from the theory of dimensions by Hilbert-Samuel series.

Using this fact, we can compute $\dim(V,0)$ by computing a standard basis of the ideal $\langle f_1, \dots, f_k\rangle$ generated in Loc$\,K[x]$ with respect to any local monomial ordering on $K[x]$. The dimension is equal to the dimension of the corresponding monomial ideal (which is a combinatorial problem).

For example, the dimension of the affine variety $V = V(yx-y, zx-z)$ is 2 but the dimension of the singularity $(V,0)$ (that is, the dimension of $V$ at the point 0) is 1:

$V : y(x-1) = z(x-1) = 0$,
$\dim(V,0) = 1,\; \dim V = 2$

Using SINGULAR we compute first the global dimension with the degree reverse lexicographical ordering denoted by dp and then the local dimension at 0 using the negative degree reverse lexicographical ordering denoted by ds. Note that in the local ring $K[x,y]_{\langle x,y\rangle}$ (represented by the ordering ds) $x-1$ is a unit.

ring R   = 0,(x,y,z),dp;  //global ring
ideal i  = yx-y,zx-z;
ideal si = groebner(i);
si;
==> si[1]=xz-z,           //leading ideal of i is <xz,xy>  
==> si[2]=xy-y
dim(si);
==> 2                     //global dimension = dim R/<xz,xy>

ring r   = 0,(x,y,z),ds;  //local ring
ideal i  = yx-y,zx-z;
ideal si = groebner(i);
si;
==> si[1]=y               //leading ideal of i is <y,z>
==> si[2]=z
dim(si);
==> 1                     //local dimension = dim r/<y,z>