


Next: Effective Construction of Algebraic
Up: Examples
Previous: Non-normal locus
We want to compute the integral closure of the Jacobian ideal 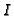 of
the
of
the 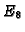 -singularity defined by
-singularity defined by
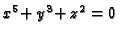 . Again, we
set the printlevel sufficiently high to get intermediate results and
comments, which are partly reproduced.
. Again, we
set the printlevel sufficiently high to get intermediate results and
comments, which are partly reproduced.
LIB "reesclos.lib";
ring A = 0,(x,y,z),dp;
ideal I = jacob(x5+y3+z2); // the Jacobian ideal
Let us first compute the Rees algebra of 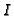 .
.
list rees = ReesAlgebra(I);
def Rees = rees[1];
setring Rees;
reesid;
==> reesid[1]=3*y^2*U(3)-2*z*U(2)
==> reesid[2]=5*x^4*U(3)-2*z*U(1)
==> reesid[3]=5*x^4*U(2)-3*y^2*U(1)
def At = rees[2]; setring At;
reesmap;
==> reesmap[1]=x reesmap[2]=y reesmap[3]=z
==> reesmap[4]=5x4t reesmap[5]=3y2t reesmap[6]=2zt
![$ \mathbf{Q}[x,y,z,U_1,U_2,U_3]/$](img259.gif) reesid is isomorphic to the Rees
algebra
reesid is isomorphic to the Rees
algebra
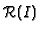 as subalgebra of
as subalgebra of
![$ \mathbf{Q}[x,y,z,t]$](img260.gif) ,
under the map
Let us now compute the integral closure of I:
,
under the map
Let us now compute the integral closure of I:
list norI = normalI(I);
After 3 iterations we reach the normalization of the Rees algebra as
![$ Q[T_1,\dots ,T_7]$](img264.gif) modulo the ideal
modulo the ideal
==> 4*T(4)*T(5)-15*T(7)^2
==> 5*T(1)^2*T(7)-2*T(2)*T(4)
==> 3*T(2)^2*T(6)-2*T(3)*T(5)
==> 2*T(1)^2*T(5)-3*T(2)*T(7)
==> 4*T(1)*T(4)*T(5)*T(7)-15*T(1)*T(7)^3
==> T(1)^2*T(2)*T(6)-T(3)*T(7)
==> 5*T(1)^4*T(6)-2*T(3)*T(4)
Now we have to determine the map
![$ Q[T_1,\dots,T_7] \to
A[t]$](img265.gif) . This is computed
by representing the ring variables
. This is computed
by representing the ring variables
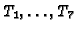 as fractions
in the variables of the Rees algebra. We get
as fractions
in the variables of the Rees algebra. We get
==> T(1) : 25*x^9*z
==> T(2) : 25*x^8*y*z
==> T(2) : 25*x^8*z^2
==> T(2) : 25*x^8*z*U(1)
==> T(2) : 15*x^4*y^2*z*U(1)
==> T(2) : 10*x^4*z^2*U(1)
==> T(2) : 10*x^6*y*z*U(1)
with the ``universal'' denominator: 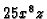 .
Since
.
Since
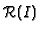 is the image under the map
is the image under the map
![$ \mathbf{Q}[x,y,z,U_1,U_2,U_3] \longrightarrow \mathbf{Q}[x,y,z,t]$](img268.gif) ,
,
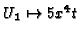 ,
,
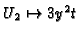 ,
,
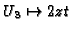 ,
,
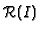 is generated in
is generated in
![$ Q[x,y,z,t]$](img272.gif) by
by
==> generator 1 : x generator 2 : y
==> generator 3 : z generator 4 : 5x4t
==> generator 5 : 3y2t generator 6 : 2zt
==> generator 7 : 2x2yt
That is,
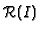 is generated in
is generated in 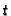 -degree 1 and, hence,
-degree 1 and, hence,
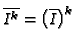 for
all
for
all 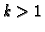 .
In particular, the integral closure of
.
In particular, the integral closure of
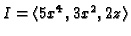 is generated by 4 elements, the extra element being
is generated by 4 elements, the extra element being 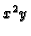 . This
result is stored in the first entry of the list norI:
. This
result is stored in the first entry of the list norI:
norI[1];
==> _[1]=5x4 _[2]=3y2 _[3]=2z _[4]=2x2y



Next: Effective Construction of Algebraic
Up: Examples
Previous: Non-normal locus
Christoph Lossen
2001-03-21