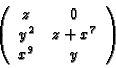Outline
Examples
Ext
Primdec
Normalize
MuPAD
Deform
Classify
Monodromy
Kodaira
Puiseux
|
Kernel of the Kodaira-Spencer Map for Space Curve Singularities I
- find a versal family of semiquasihomogenous singularities with this
fixed initial part
- compute the kernel of the
Kodaira-Spencer map of this family.
LIB "spcurve.lib";
ring r=0,(x,y,z),ds;
matrix M[3][2]=z,0,y^2,z+x^7,x^9,y;
list l=matrixT1(M,3);
Def_Posweight(l[1],std(l[2]),0);
_[1]:
_[1,1]=z
_[1,2]=x^4*T(2)+x^5*T(5)+x^6*T(7)
_[2,1]=y^2+x^11*T(1)+x^6*y*T(3)+x^12*T(4)+x^13*T(6)+x^14*T(8)
_[2,2]=z+x^7
_[3,1]=x^9
_[3,2]=y
_[2]: 1,2,2,4,5,7,8,10
setring r;
KS_Kernel(M);
_[1]=T(1)*x^14*gen(3)
_[2]=3*T(1)*x^13*gen(3)+6*T(2)*x^6*gen(2)+ ...
_[3]=3*T(1)*x^12*gen(3)+6*T(2)*x^5*gen(2)+ ...
_[4]=T(1)*x^11*gen(3)+2*T(2)*x^4*gen(2)+ ...

|