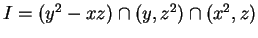| Task: | Decompose the variety defined by |
I=(y2z2-x2y3-xz3+x3yz
, y2z-xz2)
| into its irreducible components via primary decomposition. |
LIB "primdec.lib";
ring r=0,(x,y,z),dp;
ideal i=y^2*z^2-x^2*y^3-x*z^3+x^3*y*z,y^2*z-x*z^2;
primdecGTZ(i);
[1]:
[1]:
_[1]=-y2+xz
[2]:
_[1]=-y2+xz
[2]:
[1]:
_[1]=z2
_[2]=y
[2]:
_[1]=z
_[2]=y
[3]:
[1]:
_[1]=z
_[2]=x2
[2]:
_[1]=z
_[2]=x
The result we got is a list of 3 tuples of ideals, where the
first ideals are the primary and the second ideals are the
corresponding prime ideals. Hence,