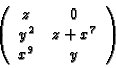|
Moduli Spaces for Space Curve Singularities - An Example
Example: quasihomogeneous
space curve singularity
with presentation matrix
ring r = 0,(x,y,z),ds;
matrix M2[3][2] = z, 0, y^2, z-x^7, x^9, y;
LIB "spcurve.lib";
LIB "stratify.lib";
minor(M2,2);
|
==>
|
_[1]=z2-x7z
_[2]=yz
_[3]=-y3+x9z-x16
|
The corresponding space curve has 2 branches given by
(y3+x16,z), resp. by
(z-x7,y). This can be seen, for instance by
using primdecGTZ(minor(M2,2)).
We compute a
monomial basis of T1:
list li=matrixT1(M2,3);
vdim(std(li[2])); //
Tjurina number
Next, we compute a versal family with fixed quasihomogeneous
initial part:
posweight(li[1],std(li[2]),0);
|
==>
|
[1]: _[1,1]=z
_[1,2]=x^4*T(3)+x^5*T(2)+x^6*T(1)
_[2,1]=y^2+x^6*y*T(4)+x^11*T(8)+x^12*T(7)+x^13*T(6)+x^14*T(5)
_[2,2]=z-x^7
_[3,1]=x^9
_[3,2]=y
[2]:
8,5,2,2,10,7,4,1
|
The kernel of the Kodaira-Spencer map can be computed by
setring r;
def KS=KSpencerKernel(M2);
We change to the ring in the variables T(i) and define the
integer vectors indicating the filtration
ring rt=0,(T(1..8)),wp(8,5,2,2,10,7,4,1);
def KS=imap(reneu,KS);
intvec wr=10,8,7,5,4,2,2,1;
intvec ws=9,6,3,0;
int step=3;
Finally, we compute the stratification:
list l=stratify(KS,wr,ws,step);
size(l);
Result: 12 Strata
|