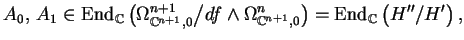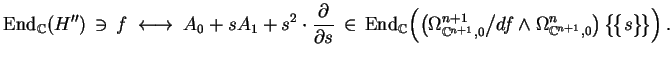|
M. Saito's A0 and
A1
| Task: |
Compute M. Saito's endomorphisms
which satisfy:
A1 is semisimple with eigenvalues being the spectral
numbers of f added by 1, and
|
ring R=0,(x,y),ds;
poly f=x5+x2y2+y5;
LIB "gaussman.lib";
The command tmatrix(f) returns a list
L :
-
L[1] contains
A0 with respect to the basis
matrix(L[4])*L[3] of H''/H'.
-
L[2] contains
A1 with respect to the basis
matrix(L[4])*L[3] of H''/H'.
-
L[4] contains a monomial vector space basis for
H''/H'.
list L=tmatrix(f);
print(L[1]); // the matrix A_0
|
==>
|
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,
1,0,0,0,0,0,0,0,0,0,0
|
print(L[2]); // the matrix A_1
|
==>
|
1/2,0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 7/10,0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 7/10,0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 9/10,0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 9/10,0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 11/10,0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 11/10,0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 13/10,0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 13/10,0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3/2
|
print(matrix(L[4])*L[3]); // the chosen basis of H''/H'
|
==>
|
-1+2xy-1445/64y5, 16x+125y4, 16y+125x4, 4x2+5y3, 4y2+5x3, xy+85/8y5, y3, x3, y4, x4, 1/2y5
|
|