
|
Common Transversals and Tangents - First
computational approach
The ideal describes all quadrics Q satisfying the conditions.
In particular, it also contains three trivial cases which have to be
removed:
|
• Q of rank 1:
|
ideal E1 of all 2-minors of the
matrix of Q ;
|
|
• Q = 2 planes meeting in L1:
|
ideal E2=<a,b,c,d,e,f,g>
|
|
• Q = 2 planes meeting in L2:
|
ideal E3=<c,d,f,g,h,k,l>
|
These excess components are removed by saturation of
I w.r.t E1, E2 and E3 in
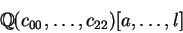 .
Computational Problem:
Even a standard basis of I cannot be computed in reasonable time because of
the large number of parameters (= 9)!
But saturation involves several standard basis computations.
Consequence:
Using this approach, the computation is infeasable.
A Different Approach
|

 .
.