AG Codes: Algorithmus
INPUT 1:
- (1)
- Bestimme alle nicht-singulären Stellen
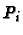 (bis zu einer
gegebenen Ordnung) und alle abgeschlossenen singulären Punkte der
projektiven ebenen Kurve
(bis zu einer
gegebenen Ordnung) und alle abgeschlossenen singulären Punkte der
projektiven ebenen Kurve 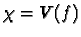 , sowie die
Hamburger-Noether-Entwicklung der jeweiligen Zweige
, sowie die
Hamburger-Noether-Entwicklung der jeweiligen Zweige 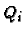 (eventuell
Körpererweiterung nötig) und berechne den Konduktor von
(eventuell
Körpererweiterung nötig) und berechne den Konduktor von 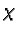 .
.
- (2)
- Finde eine
Kurve
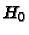 , sodass der Schnittdivisor
, sodass der Schnittdivisor
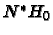 von
von 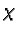 und
und 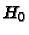 der
Ungleichung
der
Ungleichung
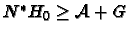 genügt.
genügt.
- (3)
- Berechne eine Basis von
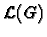 unter Verwendung
des Satzes von Brill-Noether.
unter Verwendung
des Satzes von Brill-Noether.
- (4)
- Berechne den zugehörigen evaluierenden, bzw. residuellen, Code.
Mit denselben Mitteln läßt sich auch die Weierstraß-Halbgruppe
von
![]() berechnen.
berechnen.