
| Classify |
| Coding |
| Deformations |
| Equidim Part |
| Existence |
| Finite Groups |
| Flatness |
| Genus |
| Hilbert Series |
| Membership |
| Monodromy |
| Normalization |
| Primdec |
| Puiseux |
| Plane Curves |
| Solving |
| Space Curves |
| Spectrum |
C is given by the 2x2-minors of the matrix:
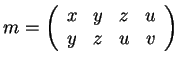 |
|
|
|
versal(f0);
|