SINGULAR Examples

Hilbert Series

Membership

Hilbert Series

Let M be a graded module over K[x₁,...,x_n] with respect to weights w₁,...,w_n .

The Hilbert function H_M is defined (on Z) by H_M(k) := dim_KM_k .

The Hilbert-Poincaré series of M is the power series

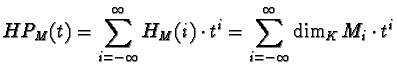
$$\displaystyle HP_M(t) = \sum_{i=$

It turns out that HP_M(t) can be written in two useful ways for weights (1,...,1) :

$$\displaystyle HP_M(t) = \frac{Q(t)}{(1-t)^n}=\frac{P(t)}{(1-t)^{\dim(M)}} </DIV> <BR CLEAR=$

where Q(t) and P(t) are polynomials with coefficients in Z.

For general w₁,...,w_n :

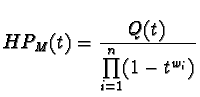
$$\displaystyle HP_M(t) = \frac{Q(t)}{\prod\limits_{i=$

where Q(t) is a polynomial in Z[t], the first (weighted) Hilbert series of M . An Example

Lille, 08-07-02