
| Classify |
| Coding |
| Deformations |
| Equidim Part |
| Existence |
| Finite Groups |
| Flatness |
| Genus |
| Hilbert Series |
| Membership |
| Monodromy |
| Normalization |
| Primdec |
| Puiseux |
| Plane Curves |
| Solving |
| Space Curves |
| Spectrum |
Compute the (first and second) Hilbert series of a homogeneous ideal.
|
Twisted cubic in P3 :
1st Hilbert series: This result can be used to compute the Hilbert polynomial H of
M = K[x,y,z,w] / I :
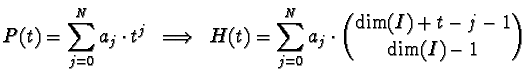
Hilbert polynomial: |