
| Classify |
| Coding |
| Deformations |
| Equidim Part |
| Existence |
| Finite Groups |
| Flatness |
| Genus |
| Hilbert Series |
| Membership |
| Monodromy |
| Normalization |
| Primdec |
| Puiseux |
| Plane Curves |
| Solving |
| Space Curves |
| Spectrum |
The ideal of a space curve singularity X is generated by the maximal minors of its presentation matrix M:
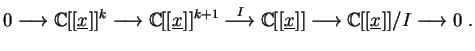
Any deformation of X is given by a perturbation of M.

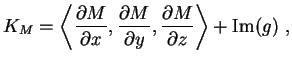
Stratification - An Example