|
|
5.1.156 vandermonde
Syntax:
vandermonde ( ideal_expression, ideal_expression,
int_expression )
Type:
- poly
Purpose:
- vandermonde(p,v,d) computes the (unique) polynomial of degree
d with prescribed values v[1],...,v[N] at the points
p
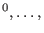 p p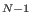 , N=(d+1) , N=(d+1)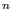 , , 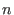 the
number of ring variables. the
number of ring variables.
The returned polynomial is
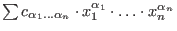 , where the coefficients , where the coefficients
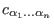 are the solution of the (transposed)
Vandermonde system of linear equations are the solution of the (transposed)
Vandermonde system of linear equations
Note:
- the ground field has to be the field of rational
numbers. Moreover, ncols(p)==
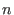 , the number of variables in the
basering, and all the given generators have to be numbers different from
0,1 or -1. Finally, ncols(v)==(d+1) , the number of variables in the
basering, and all the given generators have to be numbers different from
0,1 or -1. Finally, ncols(v)==(d+1)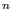 , and all given generators have
to be numbers. , and all given generators have
to be numbers. Example:
| | ring r=0,(x,y),dp;
// determine f with deg(f)=2 and with given values v of f
// at 9 points: (2,3)^0=(1,1),...,(2,3)^8=(2^8,3^8)
// valuation point: (2,3)
ideal p=2,3;
ideal v=1,2,3,4,5,6,7,8,9;
poly ip=vandermonde(p,v,2);
ip[1..5]; // the 5 first terms of ip:
==> -1/9797760x2y2-595/85536x2y+55/396576xy2+935/384x2-1309/3240xy
// compute value of ip at the point 2^8,3^8, result must be 9
subst(subst(ip,x,2^8),y,3^8);
==> 9
|
|