Home Online Manual
Top
Back: Singularity Theory
Forward: Critical points
FastBack: Algebraic dependence
FastForward: Invariant Theory
Up: Singularity Theory
Top: Singular Manual
Contents: Table of Contents
Index: Index
About: About this document

A.4.1 Milnor and Tjurina number

The Milnor number, resp. the Tjurina number, of a power series f in $K[[x_1,\ldots,x_n]]$is

\begin{displaymath} \hbox{milnor}(f) = \hbox{dim}_K(K[[x_1,\ldots,x_n]]/\hbox{jacob}(f)), \end{displaymath}

respectively

\begin{displaymath} \hbox{tjurina}(f) = \hbox{dim}_K(K[[x_1,\ldots,x_n]]/((f)+\hbox{jacob}(f))) \end{displaymath}

wherejacob(f) is the ideal generated by the partials of f. tjurina(f) is finite, if and only if f has an isolated singularity. The same holds for milnor(f) if K has characteristic 0. SINGULAR displays -1 if the dimension is infinite.

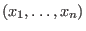SINGULAR cannot compute with infinite power series. But it can work in $\hbox{Loc}_{(x)}K[x_1,\ldots,x_n]$,the localization of $K[x_1,\ldots,x_n]$at the maximal ideal $(x_1,\ldots,x_n)$.To do this, one has to define a ring with a local monomial ordering such as ds, Ds, ls, ws, Ws (the second letter 's' referring to power 's'eries), or an appropriate matrix ordering. See Monomial orderings for a menu of possible orderings.

For theoretical reasons, the vector space dimension computed over the localization ring coincides with the Milnor (resp. Tjurina) number as defined above (in the power series ring).

We show in the example below the following:

  • set option prot to have a short protocol during standard basis computation
  • define the ring r1 of characteristic 32003 with variables x,y,z, monomial ordering ds, series ring (i.e., K[x,y,z] localized at (x,y,z))
  • list the information about r1 by typing its name
  • define the integers a,b,c,t
  • define a polynomial f (depending on a,b,c,t) and display it
  • define the jacobian ideal i of f
  • compute a standard basis of i
  • compute the Milnor number (=250) with vdim and create and display a string in order to comment the result (text between quotes " "; is a 'string')
  • compute a standard basis of i+(f)
  • compute the Tjurina number (=195) with vdim
  • then compute the Milnor number (=248) and the Tjurina number (=195) for t=1
  • reset the option to noprot
See also sing_lib for the library commands for the computation of the Milnor and Tjurina number.

 
  option(prot);
  ring r1 = 32003,(x,y,z),ds;
  r1;
==> //   characteristic : 32003
==> //   number of vars : 3
==> //        block   1 : ordering ds
==> //                  : names    x y z
==> //        block   2 : ordering C
  int a,b,c,t=11,5,3,0;
  poly f = x^a+y^b+z^(3*c)+x^(c+2)*y^(c-1)+x^(c-1)*y^(c-1)*z3+
           x^(c-2)*y^c*(y^2+t*x)^2;
  f;
==> y5+x5y2+x2y2z3+xy7+z9+x11
  ideal i=jacob(f);
  i;
==> i[1]=5x4y2+2xy2z3+y7+11x10
==> i[2]=5y4+2x5y+2x2yz3+7xy6
==> i[3]=3x2y2z2+9z8
  ideal j=std(i);
==> 7(2)s8s10s11s12s(3)s13(4)s(5)s14(6)s(7)15--.s(6)-16.-.s(5)17.s(7)s--s18(6\
   ).--19-..sH(24)20(3)...21....22....23.--24-
==> product criterion:10 chain criterion:69
  "The Milnor number of f(11,5,3) for t=0 is", vdim(j);
==> The Milnor number of f(11,5,3) for t=0 is 250
  j=i+f;    // override j
  j=std(j);
==> 7(3)s8(2)s10s11(3)ss12(4)s(5)s13(6)s(8)s14(9).s(10).15--sH(23)(8)...16...\
   ...17.......sH(21)(9)sH(20)16(10).17...........18.......19..----..sH(19)
==> product criterion:10 chain criterion:53
  vdim(j);  // compute the Tjurina number for t=0
==> 195
  t=1;
  f=x^a+y^b+z^(3*c)+x^(c+2)*y^(c-1)+x^(c-1)*y^(c-1)*z3
    +x^(c-2)*y^c*(y^2+t*x)^2;
  ideal i1=jacob(f);
  ideal j1=std(i1);
==> 7(2)s8s10s11s12s13(3)ss(4)s14(5)s(6)s15(7).....s(8)16.s...s(9)..17.......\
   .....s18(10).....s(11)..-.19.......sH(24)(10).....20...........21........\
   ..22.............................23...............................24.----\
   ------.25.26
==> product criterion:11 chain criterion:83
  "The Milnor number of f(11,5,3) for t=1:",vdim(j1);
==> The Milnor number of f(11,5,3) for t=1: 248
  vdim(std(j1+f));   // compute the Tjurina number for t=1
==> 7(16)s8(15)s10s11ss(16)-12.s-s13s(17)s(18)s(19)-s(18).-14-s(17)-s(16)ss(1\
   7)s15(18)..-s...--.16....-.......s(16).sH(23)s(18)...17..........18......\
   ...sH(20)17(17)....................18..........19..---....-.-.........20.\
   -----...s17(9).........18..............19..-.......20.-......21.........s\
   H(19)16(5).....18......19.-----
==> product criterion:15 chain criterion:174
==> 195
  option(noprot);