|
|
A.4.5 Deformations
-
The libraries
sing.lib, respextively deform.lib, contain
procedures to compute total and base space of the miniversal (= semiuniversal)
deformation of an isolated complete intersection singularity, respectively
of an arbitrary isolated singularity.
-
The procedure
deform in sing.lib returns a matrix whose columns
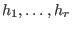 represent all 1st order deformations. More precisely, if represent all 1st order deformations. More precisely, if
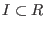 is the ideal generated by is the ideal generated by 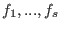 , then any infinitesimal
deformation of , then any infinitesimal
deformation of 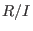 over over
![$K[\varepsilon]/(\varepsilon^2)$](sing_414.png) is given
by is given
by
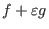 ,
where ,
where
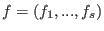 , and where , and where 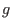 is a is a 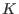 -linear combination of
the -linear combination of
the 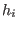 . . -
The procedure
versal in deform.lib computes a formal
miniversal deformation up to a certain order which can be
prescribed by the user. For a complete intersection the 1st order
part is already miniversal.
-
The procedure
versal extends the basering to a new ring with
additional deformation parameters which contains the equations for the
miniversal base space and the miniversal total space.
-
There are default names for the objects created, but the user may also
choose their own names.
-
If the user sets
printlevel=2; before running versal, some
intermediate results are shown. This is useful since versal
is already complicated and might run for some time on more
complicated examples. (type help versal;)
We compute for the same examples as in the section T1 and T2
the miniversal deformations:
| | LIB "deform.lib";
ring R=32003,(x,y,z),ds;
//----------------------------------------------------
// hypersurface case (from series T[p,q,r]):
int p,q,r = 3,3,4;
poly f = x^p+y^q+z^r+xyz;
print(deform(f));
==> z3,z2,yz,xz,z,y,x,1
// the miniversal deformation of f=0 is the projection from the
// miniversal total space to the miniversal base space:
// { (A,B,C,D,E,F,G,H,x,y,z) | x3+y3+xyz+z4+A+Bx+Cxz+Dy+Eyz+Fz+Gz2+Hz3 =0 }
// --> { (A,B,C,D,E,F,G,H) }
//----------------------------------------------------
// complete intersection case (from series P[k,l]):
int k,l =3,2;
ideal j=xy,x^k+y^l+z2;
print(deform(j));
==> 0,0, 0,0,z,1,
==> y,x2,x,1,0,0
def L=versal(j); // using default names
==> // smooth base space
==> // ready: T_1 and T_2
==>
==>
==> // 'versal' returned a list, say L, of four rings. In L[1] are stored:
==> // as matrix Fs: Equations of total space of the miniversal deformation\
,
==> // as matrix Js: Equations of miniversal base space,
==> // as matrix Rs: syzygies of Fs mod Js.
==> // To access these data, type
==> def Px=L[1]; setring Px; print(Fs); print(Js); print(Rs);
==>
==> // L[2] = L[1]/Fo extending Qo=Po/Fo,
==> // L[3] = the embedding ring of the versal base space,
==> // L[4] = L[1]/Js extending L[3]/Js.
==>
def Px=L[1]; setring Px;
show(Px); // show is a procedure from inout.lib
==> // ring: (ZZ/32003),(A,B,C,D,E,F,x,y,z),(ds(6),ds(3),C);
==> // minpoly = 0
==> // objects belonging to this ring:
==> // Rs [0] matrix 2 x 1
==> // Fs [0] matrix 1 x 2
==> // Js [0] matrix 1 x 0
listvar(matrix);
==> // Rs [0] matrix 2 x 1
==> // Fs [0] matrix 1 x 2
==> // Js [0] matrix 1 x 0
// ___ Equations of miniversal base space ___:
Js;
==>
// ___ Equations of miniversal total space ___:
Fs;
==> Fs[1,1]=xy+Ez+F
==> Fs[1,2]=y2+z2+x3+Ay+Bx2+Cx+D
// the miniversal deformation of V(j) is the projection from the
// miniversal total space to the miniversal base space:
// { (A,B,C,D,E,F,x,y,z) | xy+F+Ez=0, y2+z2+x3+D+Cx+Bx2+Ay=0 }
// --> { (A,B,C,D,E,F) }
//----------------------------------------------------
// general case (cone over rational normal curve of degree 4):
kill L;
ring r1=0,(x,y,z,u,v),ds;
matrix m[2][4]=x,y,z,u,y,z,u,v;
ideal i=minor(m,2); // 2x2 minors of matrix m
int time=timer;
// Call parameters of the miniversal base A(1),A(2),...:
def L=versal(i,0,"","A(");
==> // ready: T_1 and T_2
==> // start computation in degree 2.
==> // ** J is no standard basis
==>
==>
==> // 'versal' returned a list, say L, of four rings. In L[1] are stored:
==> // as matrix Fs: Equations of total space of the miniversal deformation\
,
==> // as matrix Js: Equations of miniversal base space,
==> // as matrix Rs: syzygies of Fs mod Js.
==> // To access these data, type
==> def Px=L[1]; setring Px; print(Fs); print(Js); print(Rs);
==>
==> // L[2] = L[1]/Fo extending Qo=Po/Fo,
==> // L[3] = the embedding ring of the versal base space,
==> // L[4] = L[1]/Js extending L[3]/Js.
==>
"// used time:",timer-time,"sec"; // time of last command
==> // used time: 0 sec
def Def_rPx=L[1]; setring Def_rPx;
Fs;
==> Fs[1,1]=-u^2+z*v+A(2)*u+A(4)*v
==> Fs[1,2]=-z*u+y*v-A(1)*u+A(4)*u
==> Fs[1,3]=-y*u+x*v+A(3)*u+A(4)*z
==> Fs[1,4]=z^2-y*u+A(1)*z+A(2)*y
==> Fs[1,5]=y*z-x*u+A(2)*x-A(3)*z
==> Fs[1,6]=-y^2+x*z+A(1)*x+A(3)*y
Js;
==> Js[1,1]=A(2)*A(4)
==> Js[1,2]=A(1)*A(4)-A(4)^2
==> Js[1,3]=-A(3)*A(4)
// the miniversal deformation of V(i) is the projection from the
// miniversal total space to the miniversal base space:
// { (A(1..4),x,y,z,u,v) |
// -u^2+x*v+A(2)*u+A(4)*v=0, -z*u+y*v-A(1)*u+A(3)*u=0,
// -y*u+x*v+A(3)*u+A(4)*z=0, z^2-y*u+A(1)*z+A(2)*y=0,
// y*z-x*u+A(2)*x-A(3)*z=0, -y^2+x*z+A(1)*x+A(3)*y=0 }
// --> { A(1..4) |
// A(2)*A(4) = -A(3)*A(4) = -A(1)*A(4)+A(4)^2 = 0 }
//----------------------------------------------------
|
|