|
|
2.3.6 Resolution
There are several commands in SINGULAR for computing free resolutions.
The most general command is res(... ,n) which determines heuristically
what method to use for the given problem. It computes the free resolution
up to the length
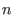 , where , where
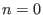 corresponds to the full resolution. corresponds to the full resolution.
Here we use the possibility to inspect the calculation process using the
option prot.
| | ring R; // the default ring in char 32003
R;
==> // characteristic : 32003
==> // number of vars : 3
==> // block 1 : ordering dp
==> // : names x y z
==> // block 2 : ordering C
ideal I = x4+x3y+x2yz,x2y2+xy2z+y2z2,x2z2+2xz3,2x2z2+xyz2;
option(prot);
resolution rs = res(I,0);
==> using lres
==> 4(m0)4(m1).5(m1)g.g6(m1)...6(m2)..
|
Disable this protocol with
When we enter the name of the calculated resolution, we get a pictorial
description of the minimized resolution where the exponents denote the rank of the
free modules. Note that the calculated resolution itself may not yet be minimal.
| | rs;
==> 1 4 5 2 0
==>R <-- R <-- R <-- R <-- R
==>
==>0 1 2 3 4
print(betti(rs),"betti");
==> 0 1 2 3
==> ------------------------------
==> 0: 1 - - -
==> 1: - - - -
==> 2: - - - -
==> 3: - 4 1 -
==> 4: - - 1 -
==> 5: - - 3 2
==> ------------------------------
==> total: 1 4 5 2
|
In order to minimize the resolution, that is to calculate the maps of the minimal
free resolution, we use the command minres:
A single module in this resolution is obtained (as usual) with the
brackets [ and ]. The print command can be used to
display a module in a more readable format:
| | print(rs[3]);
==> z3, -xyz-y2z-4xz2+16z3,
==> 0, -y2,
==> -y+4z,48z,
==> x+2z, 48z,
==> 0, x+y-z
|
In this case, the output is to be interpreted as follows: the 3rd syzygy
module of R/I, rs[3], is the rank-2-submodule of
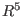 generated by the vectors generated by the vectors
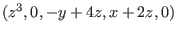 and and
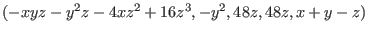 . .
|