|
|
D.5.10.7 dimH
Procedure from library sheafcoh.lib (see sheafcoh_lib).
- Usage:
- dimH(i,M,d); M module, i,d int
- Assume:
M is graded, and it comes assigned with an admissible degree
vector as an attribute, h>=l, and the basering S has
n+1 variables.
- Return:
- int, vector space dimension of
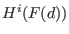 for F the coherent
sheaf on P^n associated to coker(M). for F the coherent
sheaf on P^n associated to coker(M).
- Note:
- The procedure is based on local duality as described in [Eisenbud:
Computing cohomology. In Vasconcelos: Computational methods in
commutative algebra and algebraic geometry. Springer (1998)].
Example:
| | LIB "sheafcoh.lib";
ring R=0,(x,y,z,u),dp;
resolution T1=mres(maxideal(1),0);
module M=T1[3];
intvec v=2,2,2,2,2,2;
attrib(M,"isHomog",v);
dimH(0,M,2);
==> 6
dimH(1,M,0);
==> 1
dimH(2,M,1);
==> 0
dimH(3,M,-5);
==> 36
|
See also:
sheafCoh;
sheafCohBGG.
|