|
|
4.19.4 ring operations
+
- construct a new ring
![$k[X,Y]$](sing_94.png) from from
![$k_1[X]$](sing_95.png) and and
![$k_2[Y]$](sing_96.png) .
(The sets of variables must be distinct). .
(The sets of variables must be distinct).
==,<>
- compare two rings
Note:
Concerning the ground fields
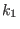 and and
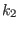 take the
following guide lines into consideration: take the
following guide lines into consideration:
- Neither
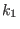 nor nor
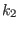 may be may be
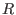 or or
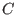 . .
- If the characteristic of
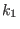 and and
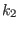 differs, then one of them must be differs, then one of them must be
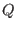 . .
- At most one of
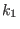 and and
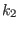 may have parameters. may have parameters.
- If one of
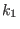 and and
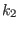 is an algebraic extension of is an algebraic extension of
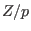 it may not be defined by a it may not be defined by a charstr of type (p^n,a).
Example:
| | ring R1=0,(x,y),dp;
ring R2=32003,(a,b),dp;
def R=R1+R2;
R;
==> // coefficients: ZZ/32003
==> // number of vars : 4
==> // block 1 : ordering dp
==> // : names x y
==> // block 2 : ordering dp
==> // : names a b
==> // block 3 : ordering C
|
ring_lib
|