Singular

5.1.11 coef

Syntax:

coef ( poly_expression, product_of_ringvars )

Type:

matrix

Syntax:

coef ( vector_expression, product_of_ringvars, matrix_name, matrix_name )

Type:

none

Purpose:

determines the monomials in f divisible by a ring variable of m (where f is the first argument and m the second argument) and the coefficients of these monomials as polynomials in the remaining variables. First case: returns a 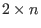matrix M, n being the number of the determined monomials. The first row consists of these monomials, the second row of the corresponding coefficients of the monomials in f. Thus,

Second case: the second matrix (i.e., the 4th argument) contains the monomials, the first matrix (i.e., the 3rd argument) the corresponding coefficients of the monomials in the vector.

Note:

coef considers only monomials which really occur in f (i.e., which are not 0), while coeffs (see coeffs) returns the coefficient 0 at the appropriate place if a monomial is not present.

Example:

ring r=32003,(x,y,z),dp; poly f=x5+5x4y+10x2y3+y5; matrix m=coef(f,y); print(m); ==> y5,y3, y, 1, ==> 1, 10x2,5x4,x5 f=x20+xyz+xy+x2y+z3; print(coef(f,xy)); ==> x20,x2y,xy, 1, ==> 1, 1, z+1,z3 vector v=[f,zy+77+xy]; print(v); ==> [x20+x2y+xyz+z3+xy,xy+yz+77] matrix mc; matrix mm; coef(v,y,mc,mm); print(mc); ==> x2+xz+x,x20+z3, ==> x+z, 77 print(mm); ==> y,1, ==> y,1