|
|
5.1.53 highcorner
Syntax:
highcorner ( ideal_expression )
highcorner ( module_expression )
Type:
- poly, resp. vector
Purpose:
- returns the smallest monomial not contained in
the ideal, resp. module, generated by the initial terms of the given
generators. If the generators are a standard basis,
this is also the smallest monomial not contained in the ideal, resp. module.
If the ideal, resp. module, is not zero-dimensional, 0 is returned.
The command works also in global orderings, but is not very useful there.
Note:
- Let the ideal I be given by a standard basis. Then
highcorner(I) returns 0 if and only if dim(I)>0 or dim(I)=-1.
Otherwise it returns the smallest monomial m not in I which has the following
properties (with
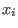 the variables of the basering): the variables of the basering):
-
if
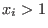 then then 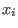 does not divide m (hence, m=1 if the ordering is global) does not divide m (hence, m=1 if the ordering is global)
-
given any set of generators
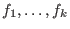 of I, let of I, let 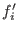 be obtained from be obtained from
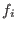 by deleting the terms divisible by by deleting the terms divisible by 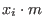 for all i with for all i with 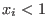 .
Then .
Then
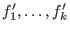 generate I. generate I.
Example:
| | ring r=0,(x,y),ds;
ideal i=x3,x2y,y3;
highcorner(std(i));
==> xy2
highcorner(std(ideal(1)));
==> 0
|
See
dim;
std;
vdim.
|