|
|
5.1.62 interred
Syntax:
interred ( ideal_expression )
interred ( module_expression )
Type:
- the same as the input type
Purpose:
- interreduces a set of polynomials/vectors.
Input: 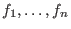
Output: 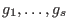 with with 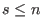 and the properties and the properties
-
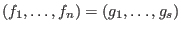 , , -
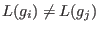 for all for all  , , -
in the case of a global ordering (polynomial ring) and
option(redSB);:
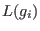 does not divide m for all monomials m of does not divide m for all monomials m of
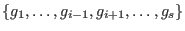 , , -
in the case of a local ordering (localization of polynomial ring) and
option(redSB);:
if
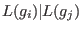 for any for any  ,then ,then
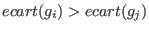 . .
Here, 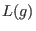 denotes the leading term of denotes the leading term of 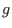 and and
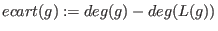 . . Example:
| | ring r=0,(x,y,z),dp;
ideal i=zx+y3,z+y3,z+xy;
interred(i);
==> _[1]=xz-z
==> _[2]=xy+z
==> _[3]=y3+xz
ring R=0,(x,y,z),ds;
ideal i=zx+y3,z+y3,z+xy;
interred(i);
==> _[1]=z+xy
==> _[2]=xy-y3
==> _[3]=x2y-y3
|
See
ideal;
module;
std.
|